Объяснение:
Алгоритм решения неравенств с двумя переменными
1. Приведем неравенство к виду f (х; у) < 0 (f (х; у) > 0; f (х; у) ≤ 0; f (х; у) ≥ 0;)
2. Записываем равенство f (х; у) = 0
3. Распознаем графики, записанные в левой части.
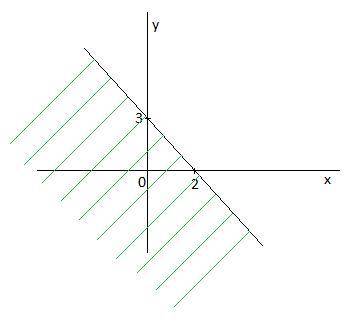
4. Строим эти графики. Если неравенство строгое (f (х; у) < 0 или f (х; у) > 0), то - штрихами, если неравенство нестрогое (f (х; у) ≤ 0 или f (х; у) ≥ 0), то - сплошной линией.
5. Определяем, на сколько частей графики разбили координатную плоскость
6. Выбираем в одной из этих частей контрольную точку. Определяем знак выражения f (х; у)
7. Расставляем знаки в других частях плоскости с учетом чередования (как по методу интервалов)
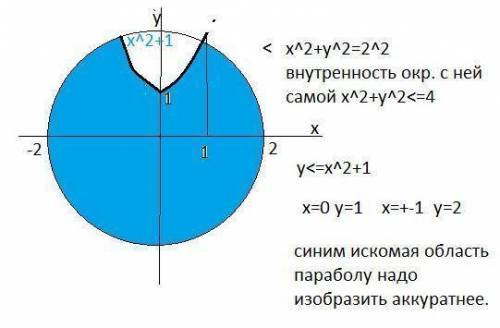
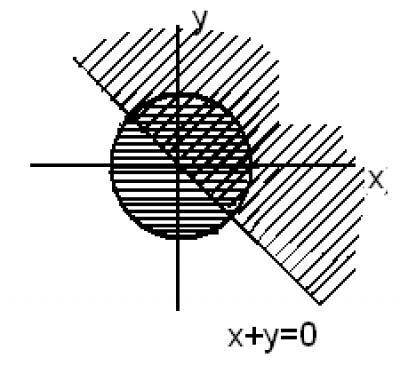
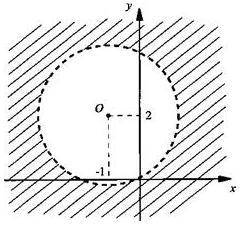
8. Выбираем нужные нам части в соответствии со знаком неравенства, которое мы решаем, и наносим штриховку
за (t+3)часов семья добирается по дороге с пробками
Известно, что скорость по дороге с пробками она на 75 км/ч меньше, чем по дороге без пробок. Составим уравнение
Приводим дроби к общему знаменателю
100(t+3)-100t=75t(t+3)
300=75t(t+3)
t²+3t-4=0
t=-4 или t=1
За один час семья добирается до дачи, расположенной на расстоянии 100 км, поэтому скорость 100 км/ч по дороге без пробок
100-75=25 км/ч скорость по дороге с пробками