Y = ln(x+5)^5 - 5x Берем первую производную: y' = 1/(x+5)^5 * 5(x+5)^4 - 5 = 5/(x+5) - 5 Так как нас интересует экстремум, то ищем такие иксы, в которых производная равна нулю: y'=0 => 5/(x+5) - 5 =0 Решив это уравнение, получаем: x=-4 Осталось проверить является ли эта точка максимумом. Если это так, то значения производной в точках, лежащих слева от x=-4 положительны, а справа - отрицательны Пусть это будут точки x=-4.5 и x=0 f'(-4.5) = 5/(-4.5+5) - 5 = 10 - 5 = 5>0; f'(0) = 5/(0+5) - 5 = 1 - 5 = -4 <0 => x=-4 - точка максимума
Решение:1)Пусть в одной части х см, тогда по условию задачи длина одного из катетов равна 4х см, а длина второго равна 3х см.2)Площадь прямоугольного треугольника равна половине произведения катетов, тогда S=·4x·3xS=24 см², тогда ·4x·3x=24 ·12x²=24 6x²=24 x²=24:6 x²=4 x=2 Получили, что в одной части 2 см, тогда длина большего катета равна 4·2=8(см), длина меньшего катета равна 3·2=6(см). ответ: 8 см, 6 см.
ответ: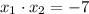 .
.