Алгебра: НУЖЕН ОТВЕТ сократить дробь 125 x^2y^3/15x^2y^4

НУЖЕН ОТВЕТ сократить дробь 125 x^2y^3/15x^2y^4

👇

Увидеть ответ

Ответ:

ffplfref

03.01.2023

1/15у

Объяснение:

1/15у

4,7(96 оценок)

Открыть все ответы

Ответ:

TamaraKengurs

03.01.2023

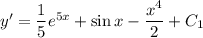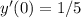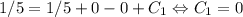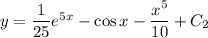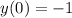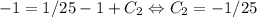1) Интегрируем обе части: $y' = \dfrac{1}{5}e^{5x}+\sin x-\dfrac{x^4}{2}+C_{1}$ . Поскольку y'(0) = 1/5 , то $1/5 = 1/5+0-0+C_{1} \Leftrightarrow C_{1} = 0$ . Интегрируем еще раз: $y = \dfrac{1}{25}e^{5x}-\cos x - \dfrac{x^{5}}{10}+C_{2}$ . Но поскольку y(0) = -1 , то $-1 = 1/25-1+C_{2} \Leftrightarrow C_{2} = -1/25$ . Следовательно, ответ: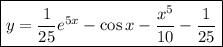 $\boxed{y = \dfrac{1}{25}e^{5x}-\cos x-\dfrac{x^{5}}{10}-\dfrac{1}{25}}$

2) Сделаем замену 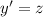y' = z . Тогда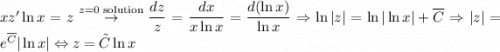 $xz'\ln x = z\stackrel{z=0\text{ solution}}{\to} \dfrac{dz}{z}=\dfrac{dx}{x\ln x} = \dfrac{d(\ln x)}{\ln x} \Rightarrow \ln|z| = \ln|\ln x|+\overline{C}\Rightarrow |z| = e^{\overline{C}}|\ln x| \Leftrightarrow z = \tilde{C}\ln x$

После обратной замены: 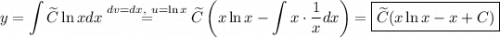$y = \displaystyle \int \widetilde{C}\ln x dx \stackrel{dv=dx,\ u=\ln x}{=} \widetilde{C}\left(x\ln x-\int x\cdot \dfrac{1}{x}dx\right) =\boxed{ \widetilde{C}(x\ln x - x+C)}$

3) Здесь снова делаем замену 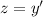z=y' . Тогда 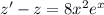$z' -z = 8x^2e^{x}$ . Решаем однородное уравнение: 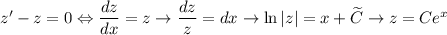$z' - z = 0 \Leftrightarrow \dfrac{dz}{dx} = z \to\dfrac{dz}{z} = dx \to \ln |z| = x+\widetilde{C} \to z = Ce^{x}$ . Применяем метод вариации постоянной, то есть ищем решение в виде 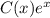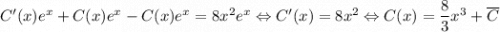$C(x)e^{x}$ : $C'(x)e^{x}+C(x)e^{x} - C(x)e^{x} = 8x^2e^{x} \Leftrightarrow C'(x) = 8x^2 \Leftrightarrow C(x) = \dfrac{8}{3}x^{3}+\overline{C}$ . Значит, 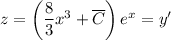$z = \left(\dfrac{8}{3}x^{3}+\overline{C}\right)e^{x} = y'$ . Здесь просто интегрируем. 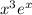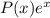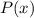Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная $x^{3}e^{x}$ имеет вид $P(x)e^{x}$ , где P(x) -- некоторый полином. 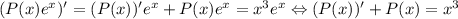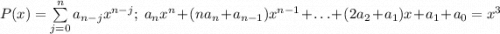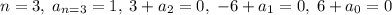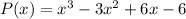Тогда $(P(x)e^{x})' = (P(x))'e^{x}+P(x)e^{x} = x^{3}e^{x} \Leftrightarrow (P(x))' +P(x) = x^{3}$ , то есть по сути, требуется решить еще один диффур, но можно поступить проще: $P(x) = \sum\limits_{j=0}^{n}a_{n-j}x^{n-j};\; a_{n}x^{n}+(na_{n}+a_{n-1})x^{n-1}+\ldots + (2a_{2}+a_{1})x+a_{1}+a_{0}=x^{3}$ , откуда $n=3,\;a_{n=3}=1,\; 3+a_{2} = 0,\; -6+a_{1}=0,\;6+a_{0}=0$ , следовательно, $P(x) = x^{3}-3x^2+6x-6$ . 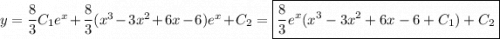Имеем: $y = \dfrac{8}{3}C_{1}e^{x}+\dfrac{8}{3}(x^{3}-3x^2+6x-6)e^{x}+C_{2} = \boxed{\dfrac{8}{3}e^{x}(x^3-3x^2+6x-6+C_{1})+C_{2}}$ , где $C_{1} = \dfrac{3}{8}\overline{C}$ .

4,6(43 оценок)

Ответ:

DeNcHiK123st

03.01.2023

Для нахождения точек пересечения с осью Х
x^4-4x^2=0
х1=0; х2=2; х3=-2;
Для нахождения экстреммумов функции нужно взять производную и прировнять ее 0
f(x)=x^4-4x^2 => f'(x)=4*x^3-8x=0
Корни: х1=0; х2=2^0.5; х3=-2^0.5; (корень квадратный из 2)
теперь нужно узнать, что это за точки минимумы или максимумы, возмем значение слева и справа от точки и подставим в уранение если знак меняется с + на - значит максимум если наоборот минимум
   -2^0.5 0 2^0.5
---*---о*о*---о*--
-2   -1 1 2

x=0 => y= 0
x=-2^0.5 => y= -4
x=2^0.5 => y= -4

x=-2 => y= 0
x=-1 => y=-3
x=1 => y=-3
x=2 => y= 0

Значение функции меняется от -2 до -2^0.5 функция убывает от 0 до -4 , а от -2^0.5 до -1 ворастает от -4 до -3 следовательно f(-2^0.5) минимум.
Значение функции меняется от -1 до 0 функция возрастает от -3 до 0 , а 0 до 1 убывает от 0 до -3 следовательно f(0) максимум.
Значение функции меняется от 1 до 2^0.5 функция убывает от -3 до -4 , а от 2^0.5 до 2 ворастает от -4 до 0 следовательно f(2^0.5) минимум.

Исследование завершено
Точки пересечения с осью Х
х1=0; х2=2; х3=-2;
Минимум
(-2^0.5;-4) и (2^0.5;-4)
Максимум
(0;0)

4,8(46 оценок)

Это интересно:

Компьютеры-и-электроника

14.03.2021

Как получить навык Водопад в игре Покемон Изумруд: полное руководство...

Хобби-и-рукоделие

04.06.2022

Голова манекена: как сделать её самому?...

Искусство-и-развлечения

05.05.2022

Как сделать костюм единорога: пошаговая инструкция...

Компьютеры-и-электроника