Из второго уравнения системы выражаем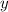 
:
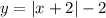
И подставляем в первое уравнение:
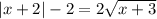
При этом нужно учитывать, что:
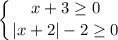
Из первого неравенства получаем, что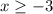 
.
Во втором неравенстве нужно рассмотреть два случая: при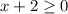 
имеем, что 
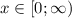, при 
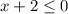получаем, что ![x \in (-\infty;-4]](/tpl/images/1357/2404/b7715.png)
. В итоге ![x \in ( - \infty; -4 ] \cup [0; + \infty)](/tpl/images/1357/2404/808c8.png)
.
В итоге получаем пересечение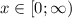 
.
Учитывая это, возводим обе части полученного ранее уравнения в квадрат и раскрываем модули:
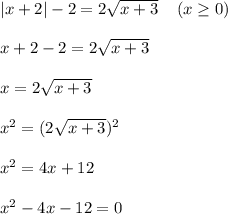
При теоремы Виета получаем, что:
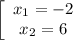
Первый корень не удовлетворяет нас по введенным ограничениям, так что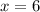 
.
Найдем :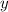
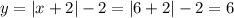
Получаем, что 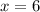и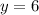 
. Эта пара удовлетворяет и первому уравнению, как можно убедиться.
Так что:
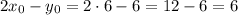
Задача решена!
ответ: 6.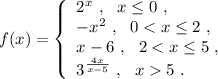
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
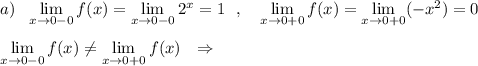
При х=0 функция имеет разрыв 1 рода .
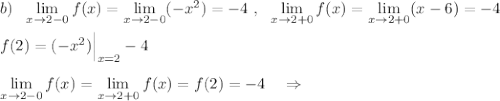
При х=2 функция непрерывна.
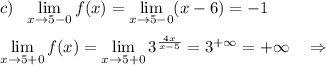
При х=5 функция имеет разрыв 2 рода .
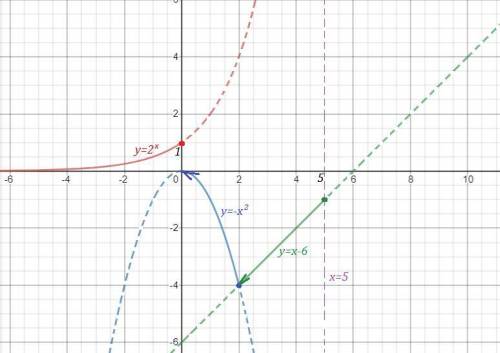
График функции нарисован сплошной линией.
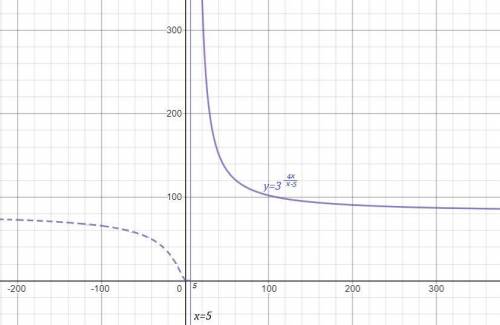
На 1 рисунке нет чертежа функции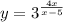 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
Объяснение:
вот на б и в не знаю ......