Объяснение:
1 Sфиг = S1 + s2 + s3 + s4 + s 5 = 6 + 1 + 1/2( 3*2 - 2*1) + 1/2(3*2)= 10+5/2 = 12.5
2 Sавсдкр = 1/2(DC * CE) +(EB * AB ) = 1/2( 12 * 5) +( 4 * 3) = 30 +12 = 42
CE = √(13^2 - 12^2) = 
BE = CE - BC = 5 - 1 = 4
AB = PE = √(AE^2 - EB^2) = √(5^2 -4^2) = √(5+4)(5-4) =√9 =3
Sавсдкр = 1/2( 12 * 5) +( 4 * 3) = 30 +12 = 42
3 Sпараллелограмма= а * в * Sin a
Sin^2 a + Cos^ a = 1
Sin a = √(1 - cos^2 a) = √(1 - 0.6^2) = √0.64 = 0.8
Sавсд = 10*16*0.8 = посчитаешь
4
5. дано ВС = 1, АВ = 2√3, ∠А = 30, ∠Д = 45
Sавсд = ?
решение : Sавсд = 1/2* (АД + ВС ) * h
Из ΔАВМ, АВ - гипотенуза, катет BM = h = 0,5*АВ = √3 (против ∡=30 )
АМ = √ (АВ^2 - h^2)= √[(2√3)^2 - (√3)^2] = √4 =2
из ΔСДН , СН = ДН = √3 ( Δ прямоугольный и равнобедренный ∠с=∠д =45)
АД = АМ + МН + НД = 2+1 +√3 = 3 + √3
Sавсд = 1/2*( 1 + 3 + √3) * √3 = √3/2( 4 + √3) = 2√3 + 1.5
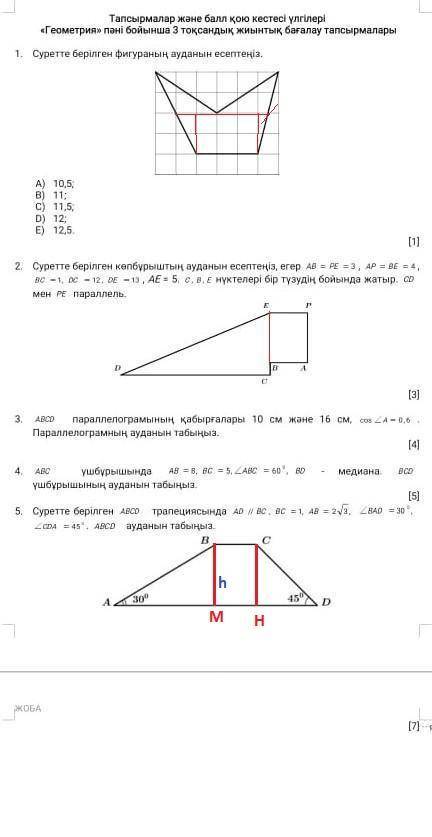
- время, за которое разгружает машину первый грузчик, мин;
- время, за которое разгружает машину второй грузчик, мин;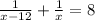
- время, за которое разгружают машину оба грузчика, мин;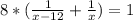
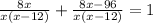
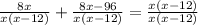
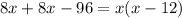
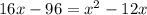
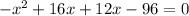
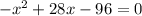
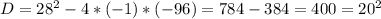
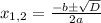
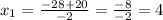
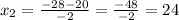
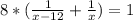
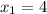не подходит, так как время не может быть отрицательным. Следовательно ответ 24.
Объяснение:
Находим нули подмодульных выражений:
х-1=0 х=1.
2х-6=0 2х=6 |÷2 x=3. ⇒
-∞____1____3____+∞
1) x∈(-∞;1)
-(x-1)+(-(2x-6))<5
-x+1-2x+6<5
-3x+7<5
3x>2 |÷3
x>2/3 ⇒
x∈(2/3;1).
2) x∈[1;3].
x-1+(-(2x-6))<5
x-1-2x+6<5
-x+5<5
x>0 ⇒
x∈[1;3].
3) x∈(3;+∞)
x-1+2x-6<5
3x-7<5
3x<12 |÷3
x<4 ⇒
x∈(3;4). ⇒
ответ: x∈(2/3;4).