Самолет летит со скоростью 504км/ч. Сколько метров он преодоливает за однц секунду Впр алгебра 2 вар 7 класс

👇

Увидеть ответ

Ответ:

ame5

29.05.2021

140 м/с

Объяснение:

1) 504 * 1000 = 504 000 м/ч

2) 504 000 / 3600 = 140 м/с

4,5(70 оценок)

Открыть все ответы

Ответ:

lllllll47900732

29.05.2021

1)2 ab-a=7 2a*( 2 +5a)-a=7 4a+10a²-a=7 10a² +3a-7=0 a1=0.7 a2=-1

b-5a=2 b=2 +5a b=2 +5a b=2 +5a b1=2+3.5=5.5 b2=2-5=-3

10a² +3a-7=0
D=9+280=289
a1=(-3+ 17)/20=14/20=0.7
a2= (-3- 17)/20 = -20/20=-1
0твет:(0.7;5.5);(-1;-3)

2)a²+b²=18 (b/9)²+b²=18 81/b²+b²=18 81+b^4-18 b²=0 b1=3 b2=-3
ab=9 a=9/b a=9/b a=9/b a1=3 a2=-3

решаем биквадратное уравнение
b^4-18 b²+81=0
обозначим b²=y
y²-18y+81=0
D/4=81-81=0
y=9
b²=9
b=+-3
ответ (3;3),(-3:-3)

4,4(70 оценок)

Ответ:

temachbatman

29.05.2021

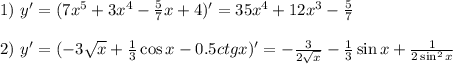
$1)~ y'=(7x^5+3x^4- \frac{5}{7} x+4)'=35x^4+12x^3-\frac{5}{7} \\ \\ 2)~ y'=(-3 \sqrt{x} + \frac{1}{3} \cos x-0.5ctg x)'=- \frac{3}{2 \sqrt{x} } -\frac{1}{3} \sin x+\frac{1}{2\sin^2x}$

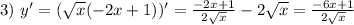
$3)~ y'=( \sqrt{x} (-2x+1))'= \frac{-2x+1}{2 \sqrt{x} } -2 \sqrt{x} = \frac{-6x+1}{2 \sqrt{x} }$

2) Найдите угловой коэффициент касательной к графику функций:
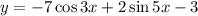а) $y=-7\cos 3x+2\sin 5x-3$ в точке с абсциссой x0=п\3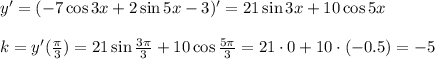

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке

$y'=(-7\cos 3x+2\sin 5x-3)'=21\sin 3x+10\cos 5x\\ \\ k=y'( \frac{\pi}{3} )=21\sin \frac{3\pi}{3} +10\cos \frac{5\pi}{3} =21\cdot 0+10\cdot(-0.5)=-5$

3. Вычислите f'(п\6), если f(x)=2cosx+x^2-пx\3 +5

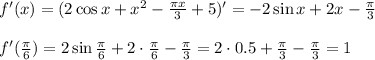
$f'(x)=(2\cos x+x^2- \frac{ \pi x}{3} +5)'=-2\sin x+2x-\frac{ \pi }{3} \\ \\ f'(\frac{ \pi }{6})=2\sin \frac{ \pi }{6}+2\cdot\frac{ \pi }{6}-\frac{ \pi }{3} =2\cdot0.5+\frac{ \pi }{3} -\frac{ \pi }{3} =1$

4. Производная от пути является скорость, т.е. s'(t) = v(t)

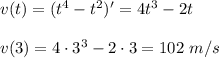
$v(t)=(t^4-t^2)'=4t^3-2t\\ \\ v(3)=4\cdot 3^3-2\cdot 3=102~ m/s$

5. Найдите все значения x, при которых выполняется неравенство f'<0, если f(x)=81x-3x^2
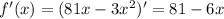
Производная функции: f'(x)=(81x-3x^2)'=81-6x

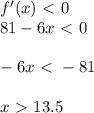
$f'(x)\ \textless \ 0\\ 81-6x\ \textless \ 0\\ \\ -6x\ \textless \ -81\\ \\ x\ \textgreater \ 13.5$

6. составьте уравнение касательных к графику функции y=x^4+x^2-2 в точках его пересечения его с осью абсцисс. Найдите точку пересечения этих касательных

Найдем точки пересечения исходной функции с осью Ох:
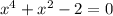
x^4+x^2-2=0

Решая это уравнение как квадратное уравнение относительно x^2, получим корни

x² = -2 - не удовлетворяет

x² = 1 откуда x0 = ±1

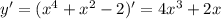
y'=(x^4+x^2-2)'=4x^3+2x

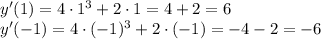
$y'(1)=4\cdot 1^3+2\cdot 1=4+2=6\\ y'(-1)=4\cdot(-1)^3+2\cdot(-1)=-4-2=-6$

Найдем теперь эти уравнения касательных
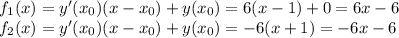
$f_1(x)=y'(x_0)(x-x_0)+y(x_0)=6(x-1)+0=6x-6\\ f_2(x)=y'(x_0)(x-x_0)+y(x_0)=-6(x+1)=-6x-6$

Приравнивая касательные, найдем точки пересечения касательных

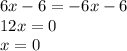
$6x-6=-6x-6\\ 12x=0\\ x=0$

(1;-6) - пересечение касательных. (см. рисунок).

7. Найдите все значения х, при которых выполняется неравенство f'=0, если f(x)=cos2x+x√3 и x э [0;4п]

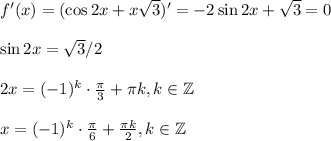
$f'(x)=(\cos 2x+x \sqrt{3} )'=-2\sin2x+\sqrt{3} =0\\ \\ \sin2x=\sqrt{3} /2\\ \\ 2x=(-1)^k\cdot \frac{\pi}{3}+ \pi k,k \in \mathbb{Z} \\ \\ x=(-1)^k\cdot \frac{\pi}{6}+ \frac{\pi k}{2} ,k \in \mathbb{Z}$

Отбор корней из x ∈ [0;4π]

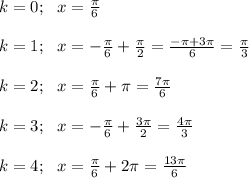
$k=0;~~ x= \frac{ \pi }{6} \\ \\ k=1;~~ x=-\frac{ \pi }{6} +\frac{ \pi }{2} =\frac{ -\pi+3 \pi }{6} =\frac{ \pi }{3} \\ \\ k=2; ~~x=\frac{ \pi }{6} + \pi =\frac{ 7\pi }{6} \\ \\ k=3; ~~ x=-\frac{ \pi }{6} +\frac{ 3\pi }{2} =\frac{ 4\pi }{3} \\ \\ k=4;~~ x=\frac{ \pi }{6} +2 \pi =\frac{ 13\pi }{6}$

8. Докажите, что функция y=(2x+5)^10 удовлетворяет соотношению 8000x^10(2x+5)^15-(y')^3=0

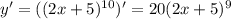
$y'=((2x+5)^{10})'=20(2x+5)^9$

$8000x^{10}(2x+5)^{15}-(y')^3=0\\ \\ y'= \sqrt[3]{8000x^{10}(2x+5)^{15}} =20(2x+5)^5x^{10/3}$

Не удовлетворяет.
$Хоть что нибуть найдите производную функции: а)y=7x^5+3x^4-5\7x +4 б)y=-3√x +1\3 cosx -1\2ctgx в)y=√$