Со скобками нужно решать, смотря какие знаки стоят в примере + или --
Объяснение:
При сложении 2 многочленов, нужно представить их в стандартном виде, потом чтобы сложить их, нужно:
1) Раскрыть скобки, не меняя знаки, потому что при + не меняется знак на противоположный.
При -- нужно опустить скобки и заменить все знаки одночленов внутри скобок на противоположные, например: 3х2-5ху-7х2у+(5ху--3х2+8х2у) =3х2-5ху-7х2у+5ху-3х2+8х2у.
Без скобок решается по разложения многочленов на множители:
1. Вынесение общего множителя за скобки
10а+25b
группировки
сокращённого умножения.
Да и ты можешь посмотреть ролики в интернете, найми репетитора.
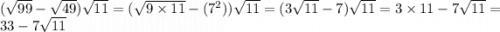
разбиваем числа на множители, и смотрим что мы можем вынести (вынести что-то из под корня можно только когда мы умножаем)
далее умножаем корень из 11 на каждый множитель, 3 корня из 11 на корень из 11, корни сокращаются получаем 3 умножить на 11.
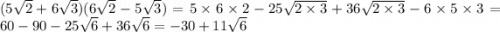
там где подкоренное число одинаковое, корень убирается, там где разное, числа под корнем умножаются
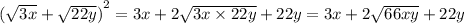
здесь открываем по формуле суммы квадрата
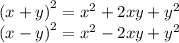
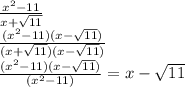
избавляемся от иррациональности
для этого домножим знаменатель и числитель на сопряженное знаменятеля
и получим формулу разности квадратов
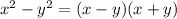
!формулы суммы квадратов не существует
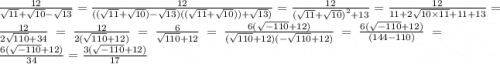
представим это в виде той самой разности квадратов в которой переменные будут выглядеть так
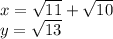
Имеем: 8m^2-6m+1=0; D=36-32=4; K(D)=2; m1=1/2; m2=1/4
Возвращаемся к замене:
1) tg^2x=1/2; tgx=K(1/2); x1=arctg(K(1/2))+Pn; или tgx=-K(1/2); x2=-arctg(K(1/2))+Pm
2) tg^2x=1/4; tgx=1/2; x1=arctg(1/2)+Pk; или tgx=-1/2; x2=-arctg(1/2)+Pr