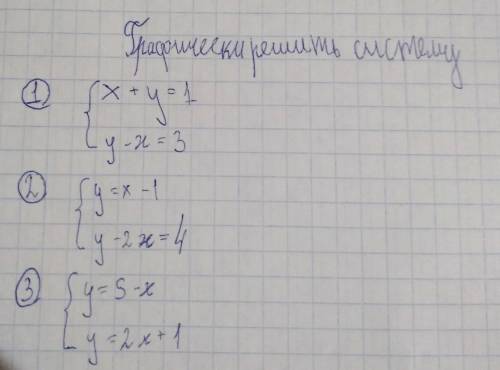
Пусть a>b>0 докажите что a³>b³, a³>ab², a⁴>a²b², a²b²>b⁴
a² - b² = (a - b)(a + b)
a³ - b³ = (a - b)(a² + ab + b²)
a>b>0 ⇒ a - b > 0 a > 0 b > 0
1. a³>b³
a³ - b³ > 0
(a - b)(a² + ab + b²) > 0 так как a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
2. a³>ab²
a³ - ab² > 0
a(a² - b²) > 0
a( a - b)(a + b) > 0 так как a и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
3, a⁴>a²b²
a⁴ - a²b² > 0
a²(a² - b²) > 0
a²(a - b)(a + b) > 0 так как a и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
4. a²b²>b⁴
a²b²- b⁴ > 0
b²(a² - b²) > 0
b²(a - b)(a + b) > 0 так как b и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
На картинках
Объяснение:
Нужно решать через уравнение
1. x + y = 1
(x=1; y=1)
y - x = 3
(-x=3; y=3)
(x=-3; y=3)
2. y = x -1
y - x = -1
(-x=-1; y=-1)
(x=1; y=-1)
И так дальше...