к.р 8 класс 1 Задание
За теоремой Виета найти корни квадратного уравнения x^2-8x+15=0
2 Задание
Не решая уравнение найти сумму и произведение корней x^2+x-6=0
3 Задание
Найти корни уравнения x^2-8*x=0
4 Задание
Найти корни уравнения x^2-49=0
5 Задание
решить уравнение 7x=x^2+12
6 Задание
решить уравнение x^2+5x= -6
7 Задание
При каких значениях x, значение многочлена x^2-2x-3 равняется 0
8 Задание
решить уравнение 2x^2+7x-4=0
9 Задание
решить уравнение x*|x|+3x-4=0
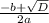 =
= 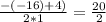 = 10
= 10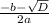 =
= 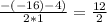 = 6
= 6
1) Поиск ОДЗ – область допустимых значений.
2) Решение уравнения.
Немного о первом.
Все семь основных арифметических действий
Происхождение такого недоразумения вполне объяснимо. Это происходит из созвучности понятий «квадратный арифметический корень» и «корни нелинейного уравнения». Выше мы говорили именно о «квадратном арифметическом корне», и об однозначности этого арифметического действия, а что такое «корни нелинейного уравнения» можно проиллюстрировать на таком примере, как
Значит при поиске ОДЗ (область допустимых значений) нужно всегда учитывать, что подкоренное выражение (всё то, что стоит под знаком корня) во-первых: должно быть неотрицательным, потому что иначе нельзя извлечь корень, а во-вторых: результат вычисления самого арифметического квадратного корня должен быть равен тоже неотрицательному числу, по причинам, которые были подробно описаны в предыдущем абзаце. Есть ещё несколько простых принципов, по которым выстраивается логика ОДЗ, но в данной задаче они не нужны, так что не будем все их перечислять. А теперь решим задачу классическим
Р Е Ш Е Н И Е :
1. ОДЗ:
2. Решение уравнения:
О Т В Е Т :