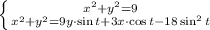
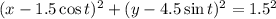 , видим, что решениями системы есть координаты точек пересечений кругов с центрами
, видим, что решениями системы есть координаты точек пересечений кругов с центрами  и
и 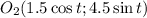 и радиусами
и радиусами 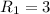 и
и 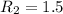 согласно. Эти круги имеют единую общую точку в таких случаях
согласно. Эти круги имеют единую общую точку в таких случаях (внешний ощупь)
(внешний ощупь)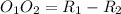 (внутренний ощупь)
(внутренний ощупь)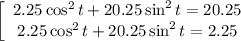
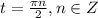 . Остается при этих значениях параметра t решить систему уравнений.
. Остается при этих значениях параметра t решить систему уравнений. решение системы будет
решение системы будет 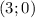
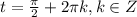 решение системы:
решение системы: 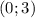
 решение системы
решение системы 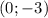
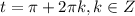 , решение системы
, решение системы 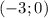
процент- это одна сотая часть числа.
1га=100м·100м=10000м²
1) 6% от 1га = (6/100)·10000=600м². а не 60м²;
2) 2,3% от 1га =(2,3/100)·10000=230м². Верно;
3) 1 ар = 100м². Его еще называют соткой.
26% от 1 ара = (26/100)·100м²=26м². Верно!
4) 250% от 1ара = (250/100)·100м²=250м², а не 25м²
5)1кв.км=1000м·1000м=1000000м²
154%от 1км²= (154/100)·1000000м²=1540000м², а не 154000м²
6) 0,7% от 1 кв.км=(0,7/100)·1000000м²= 7000м².Верно!
Принцип ясен? Непонятки еще остались?