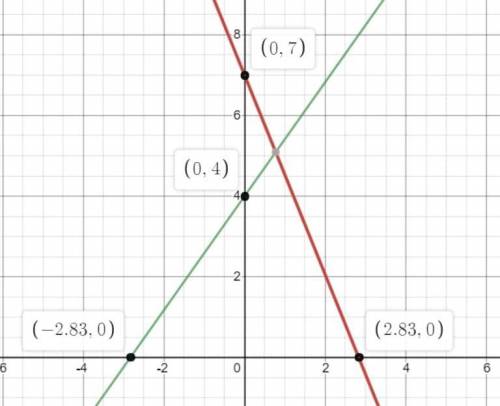
Перенесем все на координатную плоскость. Пусть точка Н = (0,0), точка А лежит на оси Оу. На скрине А(0,7), В(0,4), а рассматривать мы будем любые А(0, а) и В(0,b).
Получается, одна прямая проходит точку А и точку (-k, 0) а другая - B и (k,0), при чем мы рассматриваем всевозможные k. Здесь k - расстояние от точки Н до точки С и D.
Кстати говоря, условие, что точка В должна быть между А и Н необязательно, можно взять и точку А между В и Н, на решение это не влияет в силу симметриии, главное, что бы обе точки лежали на перпендикуляре (то есть на оси Оу).
Запишем уравнение прямых.
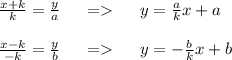
Так как нас интересует пересечение - приравниваем:
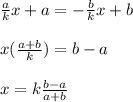
Поскольку пересечение двух прямых точно лежит на каждой из них, нужно подставить полученный икс в уравнение любой из прямых, результат будет одинаков.
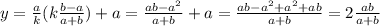
Получилось, что для любого k, то есть для любого расстояния между точкой H до С и D, мы находим зависимый от k икс, и независимый от k игрек. То есть как бы мы не раздвигали точки C и D, игрек будет всегда один и тот же, зависящий только от точек А и В, на которые мы "привязываем" прямые AD и BC.
Итого, ответ - прямая 
ответ: ОДЗ: х не равно -3; х не равно о.
переносим 3 в левую часть.
дополнительный множитель к первой дроби х, ко второй х+з, к третей х(х+3)
раскрывает скобки и у нас получается в числителе 5х+4х+12-3х^2-9х в знаменателе х(х+3)
уничтожаем подобные члены и у нас остается +12-3х^2/х(х+3)>=0
умножаем на -1 и у нас получается (когда мы умножаем на -1 знак тоже меняется)
3х^2+12/х(х+3)<=0
теперь выносим 3 и у нас получается 3(х^2-4)/х(х+3)<=0
теперь раскладываем на множители в скобке
3(х-2)(х+2)/х(х+3)<=0
воспользуемся методом интервалов,а для этого найдем нули функции
f(x)=f(0)=f(-2)=f(2)=f(-3)
теперь нули вынесем на координатную прямую
___-3-202>
ответ х=(-3;-2]u(0;2]
2. H2O+CO2+Ca(NO3)2
3. H2O+CO2+CaCl2