Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что .
Учитывая это перепишем уравнение:Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если , а .
Тогда решением исходного уравнения является пара чисел .
Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К. На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10! Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы. Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами. Для М и Т это будет 2! и 2!, для А – 3! С учётом порядка позиции их будет: Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой Перестановки с повторением. Всего у нас Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
или х₂ = 1
(см. объяснение)
Объяснение:
Рассмотрим уравнение:
Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что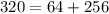
.
Учитывая это перепишем уравнение:
Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если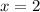
, а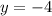 
.
Тогда решением исходного уравнения является пара чисел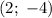
.
Уравнение решено!