
Объяснение:
ответ будет ниже в файле
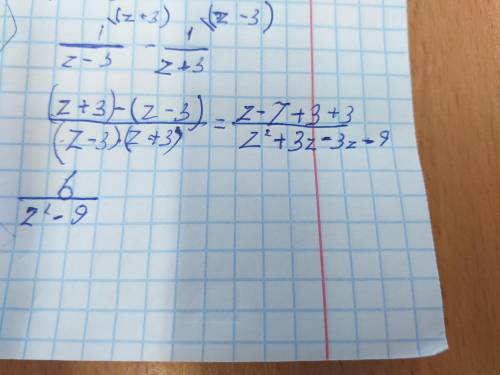
№1
а) (x-4)^2=x^2-8x+16
б) (3x-5)^2=9x-30x=25
в) (2a-3)*(2a+3)=4a^2-9
г) (y^2-2)*(y^2+2)=y^4-4
№2
а) b^2-0.36=(b-0.6)*(b+0.6)
б) y^2-6y+9=(y-3)^2
№3
(2a-3b)*3b+(a-3b)^2
a=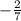
Упрощаем выражение:
6ab-9b^2+a^2-6ab+9b^2
Сокращаем все что сокращается:
a^2
Теперь решаем:
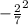
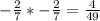
ответ: 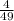
№4
а) 5(2-3xy)(2+3xy)=20-45x^2y^2
б) (a^3-b^2)^2=a^6-2*a^3*b^2+b^4
в) (x+y)^2-(x-y)^2=4xy
№5
(6a-1)(6a+1)-4a(9a+2)=-1
Упрощаем выражение:
-1-8a=-1
Данное уравнение не решаемо.
№6
(2x+3)(3x-7)-(x+1)(x-1)
Упрощаем выражение:
6x^2-5x-21-x^2+1
Снова упрощаем выражение:
5x^2-5x-20
Проверяем правильность утверждения что это выражение делится на 5 при любом целом "x"
Пусть x=8
Значит выражение теперь выглядит так:
(5*8)^2-5*8-20
Решать дальше смысла нет, так как при любом целом "x" последней цифрой будет ноль, значит выражение будет делится на 5.
Исключение это "x=1" в результате выражение будет равно 1.
Если это учесть то утверждение неверно!
Удачи, надеюсь
y=-x^2 Это квадртичная функция
График функции- парабола , ветви направлены вниз, т.к. а меньше нуля.
Это самая простая квадратичная функция (-х)^2 =х^2 (четная степень), значит функция чётная.
У параболы всегда есть вершина.Здесь это А(0;0).Наша парабола касается оси абсцисс в точке А(0;0), проходя через начало координат.
Любая парабола имеет ось симметрии. У нас это прямая х=0(ось ординат)
Чтобы построить график этой функции надо найти координаты точек
У(0)=0 У(-1)=-1
У(1)=-1 У(-2)=-4
У(2)=-4 У(-3)=-9
У(3)=-9
Можно в табличке записать
Х 0 1 2 3 4 -1 -2 -3
У 0 -1 -4 -9 -16 -1 -4 -9
Построй систему координат, а потом по точкам нарисуешь плавно параболу, только не заканчивай ветви на точках, ветви идут в бесконечность, т.к. Х может быть любым. Желаю удачи.
6/z°2-9
Объяснение:
надеюсь