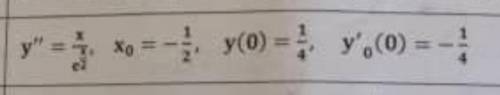
Дано:
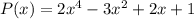

Найти 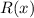 - остаток от деления
- остаток от деления 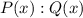
Решение.
1) Для начала разложим многочлен 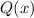 на множители, для этого решим уравнение:
на множители, для этого решим уравнение:
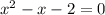
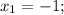

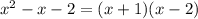
2) Так как данный многочлен 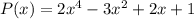 делится на
делится на 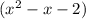 с остатком, то представим его в виде
с остатком, то представим его в виде
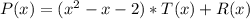
где
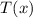 - неполное частное;
- неполное частное;
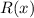 - искомый остаток.
- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
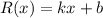
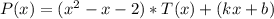
3) Подставим в равенство 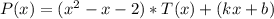 первый корень
первый корень 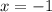 и получим:
и получим:
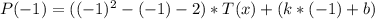
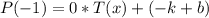
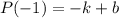
Вычислим 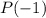 .
.
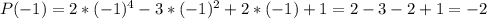
Так как 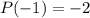 , то
, то
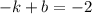 =>
=> 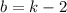
4) Аналогично решаем и со вторым корнем 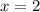 .
.
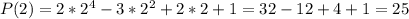
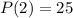
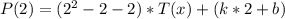
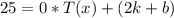
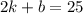
5) Подставим 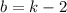 в полученное уравнение:
в полученное уравнение:
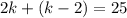
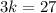
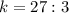
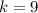
6) 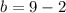
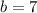
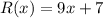 - искомый остаток.
- искомый остаток.
ответ: 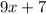
1.
1)
38² - 64 = 38² - 8² = (38 - 8)(38 +8) = 30 * 46 = 1380,
2.
1)
2в² - 18 = 2 * (в² - 9) = 2 * (в - 3)(в + 3),
3)
81х² - 18ху + у² + 63х - 7у = (81х² - 18ху + у²) + (63х - 7у) =
= (9х - у)² + 7*(9х - у) = (9х - у)(9х - у + 7),
4)
m² + n² + 2mn = (m + n)².
3.
а)
(8 - 2n)(8 + 2n) + (9 + 2n)² - 64 = 64 - 4n² + 81 + 36n + 4n² - 64 =
= 36n + 81 = 9(4n + 9),
б)
(3х - 8)² + (4х - 8)(4х + 8) = 9х² - 48х + 64 + 16х² - 64 = 25х² - 48х,
при х=-2:
25 * (-2)² - 48 * (-2) = 100 + 96 = 196,
4.
1 число - х,
2 число - (х+2),
(х+2)² - х² = 188,
х² + 4х + 4 - х² = 188,
4х = 184,
х = 46 - 1 число,
х+2 = 46+2 = 48 - 2 число
По частям:
общее решение
частное решение
При
ответ: 0,35