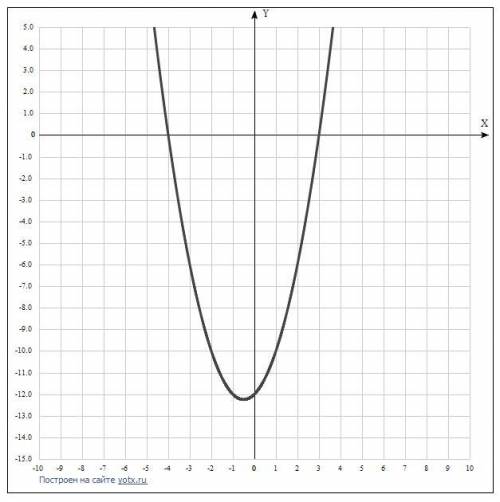
Та как (х²+х-12) - это квадратный трёхчлен, то графиком этой функции является парабола
так как а=1, то ветви параболы будут направлены вверх
Найдём точку пересечения с осью ОХ
у=0, значит х²+х-12=0; Найдём корни по теореме Виета
х ₁= -4; х₂=3
Координаты точек пересечения с осью ОХ: (-4;0) и (3;0)
Координаты точки пересечения с осью ОУ : (0; -12)
при х=0 у= 0²+0-12=-12
Найдём абсцису вершины параболы:
Хв= -1/2*1= - 1/2= -0,5
Ув= (-0,5)²-0,5-12=0,25-12,5=-12,25
Координаты вершины параболы ( -0,5; -12,25)
Ось симметрии параболы х= -0,5
Найдём ещё несколько точек для построения
х -3 2 -2 1
у -6 -6 -10 -10
Подставляем:
27*(-1)^3+8*1^3-(3*(-1)+2*1)(9*(-1)^2+6*1*(-1)+4*1^2)= -12
Когда отр. число возводим в квадрат, то минус уходит. Если же в куб, то остается.
Если Положит. число возводим в квадрат, или в куб , то оно остается положит.
Извини, объяснил как смог =)