Ймовірність якої події дорівнює дробу, значення якого більше за нуль і менше 1?

👇

Увидеть ответ

Открыть все ответы

Ответ:

Саша039

29.03.2020

Если прямая касается параболы, то коэффициент a можно рассчитать как минимум 3мя разными

1)Дискриминант

$ax^2+5x+8=-2x+1\\ax^2+7x+7=0$

-----

Если прямая касается параболы тогда дискриминант этого уравнения будет равняться нулю.

$49-4*a*7=0\\a=\frac{7}{4}$

ответ 7/4

2)Теорема виета

Не сильно отличается от первого:

$ax^2+5x+8=-2x+1\\ax^2+7x+7=0$

если прямая касается параболы, тогда квадратный трехчлен имеет всего один корень, тогда по т. виета:

$2x=-\frac{7}{a} \\x^2=\frac{7}{a}$

-------------

из 1:

$a=-\frac{7}{2x}$

подставим в 2:

$x^2=-2x\\x=-2\\----\\a=\frac{7}{4}$

-------------

ответ 7/4 (менее быстрый метод но зато нам сразу будет известна точка касания)

3)Производная

$ax^2+5x+8=-2x+1\\ax^2+7x+7=0$

если прямая касается параболы, тогда значение производной прямой в точке касания равно значению производной параболы в точке касания:

$ax^2+7x+7=0\\2ax+5=-2 a=\frac{-7}{2x}$

подставим в первое:

$\frac{-7x}{2}+7x+7=0-7x+14x+14=0x+2=0 x=-2$

a=7/4

ответ 7/4 (Опять же не самый быстрый но зато мы сразу узнаем координаты касания)

4,4(58 оценок)

Ответ:

marishakfine

29.03.2020

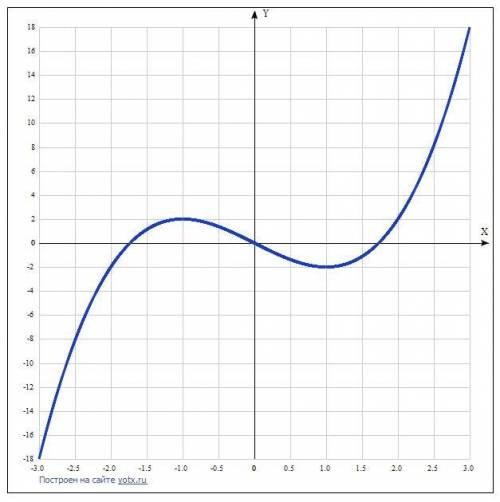
Таблица точек

x y

-3.0 -18

-2.5 -8.1

-2.0 -2

-1.5 1.1

-1.0 2

-0.5 1.4

0 0

0.5 -1.4

1.0 -2

1.5 -1.1

2.0 2

2.5 8.1

3.0 18

Точка пересечения графика функции с осью координат Y:

График пересекает ось Y, когда x равняется 0: подставляем x=0 в x³-3x.

у =0³-3*0 = 0,

Результат: y=0. Точка: (0; 0.

Точки пересечения графика функции с осью координат X:

График функции пересекает ось X при y=0, значит, нам надо решить уравнение:

x³-3x = 0

Решаем это уравнение и его корни будут точками пересечения с X:

x (х²-3) = 0,

х1 = 0, х2,3 = +-√3.

Результат: y=0. Точки: (0; -√3), (0; 0) и (0; √3).

Экстремумы функции:

Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:

y'=3x² – 3 = 0

Решаем это уравнение и его корни будут экстремумами:

3(х²-1) = 0,

х1 = 1, х2 = -1.

Результат: y’=0. Точки: (-1; 2) и (1; -2). Это критические точки.

Интервалы возрастания и убывания функции:

Найдем значения производной между критическими точками:

x = -2 -1 0 1 2

y' = 9 0 -3 0 9.

• Минимум функции в точке: х = -1,

• Максимум функции в точке: х = 1.

• Возрастает на промежутках: (-∞; -1) U (1; ∞)

• Убывает на промежутке: (-1; 1)

Точки перегибов графика функции:

Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:

y'' = 6x = 0

Отсюда точка перегиба х = 0

Точка: (0; 0).

Интервалы выпуклости, вогнутости:

Находим знаки второй производной на промежутках (-∞; 1) и (1; +∞).

х = -1 0 1

y'' = -6 0 6.

Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.

• Вогнутая на промежутках: (0; ∞),

• Выпуклая на промежутках: (-∞; 0)

Вертикальные асимптоты – нет.

Горизонтальные асимптоты графика функции: