Выразите: 2,5•10²т в граммах 1,8•10-⁵ км в сантиметрах - id1810069020221122 от NIKROSO 22.11.2022 12:44

Question

Алгебра: Выразите: 2,5•10²т в граммах 1,8•10-⁵ км в сантиметрах​

NIKROSO · Accepted Answer

Из 12 учеников, выбрать ученика, которому мы дадим первую книгу, можно После этого остается 11 учеников без книг. Из них выбрать следующего ученика, которому мы дадим вторую книгу, можно

Общее число раздать разные (!) книги существует 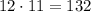$12\cdot 11=132$ .

Другими словами, мы находили размещение из 12 по 2:

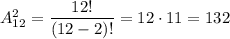
$A_{12}^2=\dfrac{12!}{(12-2)!} =12\cdot11=132$

А вот если книги были бы одинаковыми, то порядок выбора учеников был бы не важен: все выбранные ученики получили бы одинаковые книги. В этом случае мы вычисляем сочетание из 12 по 2:

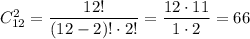
$C_{12}^2=\dfrac{12!}{(12-2)!\cdot2!} =\dfrac{12\cdot11}{1\cdot2} =66$

Итак, если учитель раздает разные книги, то существует это сделать. А соответствует случаю, если раздаваемые книги одинаковые.

ответ: 132

Выразите:2,5•10²т в граммах1,8•10-⁵ км в сантиметрах​

MOGZ ответил

Выразите:
2,5•10²т в граммах
1,8•10-⁵ км в сантиметрах