По условию скорость мотоциклиста больше скорости велосипедиста, значит,
10 км - это расстояние, которое проехал велосипедист до встречи;
тогда
50-10=40 км - это расстояние, которое проехал мотоциклист до встречи.
Пусть х км/ч - скорость велосипедиста, тогда
(х+30) км/ч - скорость мотоциклиста;
10/х ч - время движения велосипедиста до встречи;
40/(х+30) ч - время движения мотоциклиста до встречи.
По условию на движение до встречи каждый из них потратил одинаковое количество времени, получаем уравнение:

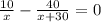
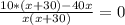
ОДЗ: x>0
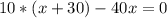



10 км/ч - скорость велосипедиста,
№1. Одна сторона прямоугольника на 2 см меньше стороны квадрата, а вторая сторона больше, чем сторона квадрата, на 4 см. Найдите сторону квадрата, если площадь прямоугольника равна 40 см².
Решение
сторона квадрата = хсм. Тогда стороны прямоугольника будут
х -2 и х +4
(х-2)(х+4) = 40
х² +2х -8 = 40
х² +2х -48 = 0
По т. Виета корни 6 и -8(не подходит по условию задачи)
ответ : сторона квадрата = 6см
№2. Найдите катеты прямоугольного треугольника, если известно, что один из них на 4 см меньше другого, а гипотенуза равна 20 см.
Один катет = х, другой = х - 4
По т. Пифагора х² + (х -4)² = 400
х² + х² -8х +16 = 400
2х² -8х -384 = 0
х² -4х -192 = 0
х = 2 +-√(4 +192) = 2 +-14
х₁ = 16 и х₂ = -12(не подходит по условию задачи)
ответ: катеты 16см и 12 см
cos2x-cos4x+3sqrt(2)cos2x-cos2x=3
3sqrt(2)cos2x-cos4x-3=0
3sqrt(2)cos2x-(2cos^(2x)-1)-3=0
3sqrt(2)cos2x-2cos^2(2x)-2=0
cos2x=t
2t^2-3sqrt(2)t+2=0
t=sqrt(2)>1 не подходит
t=sqrt(2)/2
cos2x=sqrt(2)/2
2x=+-П/4+2Пk
x=+-П/8+Пk