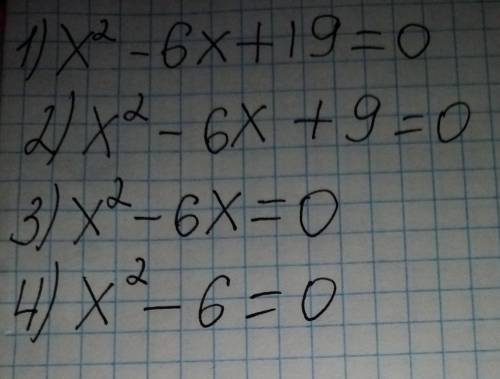
cosx=a ⇒ x=±arccosa+2πn, n∈Z
cosπ(8x+7)/3=1/2, π(8x+7)/3=±π/3+2πn
8x+7=±1+6n,
8x= -7±1+6n,
x= -7/8±1/8+6n/8= -7/8±1/8+3n/4,n∈Z
Придаём значения целому числу n^
n=0, x=-7/8-1/8=-1<0
n=1, x=-7/8-1/8+6/8=-2/8=-1/4<0 или x=-7/8+1/8+6/8=0
n=2, x=-7/8-1/8+12/8=4/8=1/2 >0 или x=-7/8+1/8+12/8=6/8=3/4
Понятно, что иксы дальше будут увеличиваться.Самое наименьшее положительное значение будет при n=2, х=1/2>0
Тут без производных не обойтись...
y' = 3x^2+6x-3 = 0
x^2+2x-1=0
x1=-1-sqrt(2) этот корень вне интервала, его не рассматриваем
x2=-1+sqrt(2) этот корень внутри интервала, его возьмём во внимание.
Дальше можно пойти двумя путями
1. Подсчитать значения у(-2), у(х2), у(1) и выбрать из них наименьший
2. Продолжить исследовать исходную функцию, может, что-то прояснится.
Пойдём 2 путём
Рассмотрев неравенство y'>0 мы найдём интервалы возрастания(и соответственно, убывания функции), наложив на них наш отрезок, получим, что функция от -2 до х2 убывает, а от х2 до 1 возрастает, так что на этом отрезке Мин функции достигается при х=х2.
осталось его найти. Это нудная процедура, так как х2 с корнем, но попробуем
х^3+3x^2-3x = x*(x^2+3x-3)=(sqrt(2)-1)*(2-2sqrt(2)+1+3sqrt(2)-3-3)=(sqrt(2)-1)*(sqrt(2)-3)= 2-sqrt(2)-3sqrt(2)+4=6-4sqrt(2)=2(3-2sqrt(2))
Ну вот, что-то получилось, это и будет ответ.
PS Перепроверь арифметику, писАл в экран, мог допустить неточность.
Успехов.
x^2-6x+19=0
a=1 b=-6 c=19
D=b^2-4ac=(-6)^2-4*1*19=36-76<0, следовательно, решений нет. ответ: решений нет.
x^2-6x+9=0
a=1 b=-6 c=9
D=b^2-4ac=(-6)^2-4*1*9=36-36=0, следовательно, ур-е имеет единственный корень, который мы можем вычислить по формуле: x=(-b)/2a=-(-6)/2*1=6/2=3 ответ: 3.
x^2-6x=0
Вынесем "х" за скобку:
x(x-6)=0
Произведение равно 0 тогда, когда хотя бы один из множителей равен 0. Следовательно:
x=0 или x-6=0 x=6 ответ: 0, 6.
x^2-6=0
x^2=6
Извлекаем квадратный корень из двух частей и получаем: