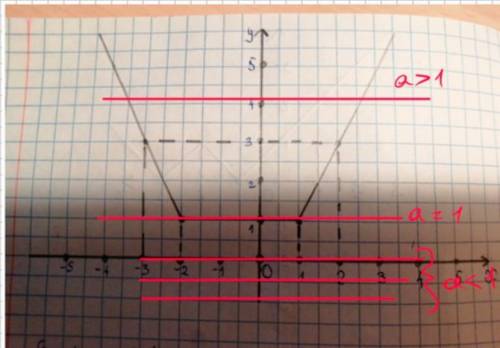
Разобьем данное уравнение на две функции , график функции уже построен на рисунке, так что объяснять как строить такой график не буду. График функции представляет собой прямую совпадающую (при a=0) с осью абсцисс или параллельной ей (при a≠0). Тогда "передвигая" прямую можем с графика ответить на вопросы к заданию. 1) не имеет решений при a<1. 2) Из графика видно что данное уравнение имеет одно, два, или ни одного решения.
3) имеет бесконечно много решение при a=1. 4) имеет два решения при a>1.
ОТВЕТ: 1)  2)
2) 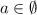 3)
3) 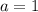 4)
4) 
cos²α = 1 - sin²α
cos²α = 1 - 576/625
cos²α = 49/625, cosα= -7/25 (перед дробью знак минус, т.к. α∈(π;3π/2) , а косинус в этом промежутке отрицательный)
2. sin (3π/2 - 2x) = sinx, (3π/2 ; 5π/2)
Применяем формулы приведения, и получаем:
-cos2x = sinx |:(-1)
cos2x = -sinx
cos²x-sin²x = -sinx
cos²x-sin²x+sinx = 0
1 - sin²x - sin²x + sinx = 0
-2sin²x + sinx + 1 =0
Делаем замену: sinx=a
-2a² + a + 1 = 0
D = 9, √D = 3
a1 = 1, a2 = - 1/2
sinx = 1 sinx = -1/2
x = π/2 + 2πn x = (-1)^n arcsin(-1/2) + πn
x=(-1)^n+1 π/6 + πn
Перебираем корни:
n=0 n=1 n=2
x=π/2 - не подходит x=5π/2 - подходит x=9π/2 - не подходит
x=-π/6 - не подходит x=7π/6 - не подходит x=11π/6 - подходит
n=3
x=13π/2 - не подходит
x=19π/6 - не подходит.
Дальше корни будут больше, и не войдут в промежуток. Значит, только 2 корня