log₇ (x² - 9) - log₇ (9 - 2x) = 1
ОДЗ :
1) x² - 9 > 0; (x + 3) (x - 3) > 0
Метод интервалов
(-3) (3) > х
x ∈ (-∞; -3) ∪ (3; +∞)
2) 9 - 2x > 0; 2x < 9; x < 4,5
ОДЗ : x ∈ (-∞; -3) ∪ (3; 4,5)
log₇ (x² - 9) = log₇ (9 - 2x) + 1
log₇ (x² - 9) = log₇ (9 - 2x) + log₇7
log₇ (x² - 9) = log₇ (7 · (9 - 2x))
x² - 9 = 7 · (9 - 2x)
x² + 14x - 72 = 0 Квадратное уравнение, корни по т. Виета
(x + 18)(x - 4) = 0
1) x + 18 = 0; x₁ = -18; x₁ ∈ (-∞; -3) ∪ (3; 4,5)
2) x - 4 = 0; x₂ = 4; x₂ ∈ (-∞; -3) ∪ (3; 4,5)
ответ: x₁ = -18; x₂ = 4
Использованы формулы
logₐ a = 1
logₐ b + logₐ d = logₐ (b · d)
(???) за 60 мин
Объяснение:
1) 1/55 кувшина за 1 мин выпивают Двалин и Бомбур
2) 1/110 кувшина за 1 мин выпивают Бомбур и Глоин
3) 1/165 кувшина за 1 мин выпивают Глоин и Двалин
4) 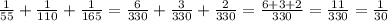
- удвоенное кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
5) 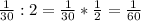
- кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
6) 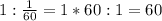
- за столько минут выпьют этот кувшин трое гномов
----------------------
ПЛОХАЯ ЗАДАЧА с кривыми данными - получается Двалин и Бомбур выпьют кувшин быстрее чем они выпьют кувшин втроем
---------------------------
=>Двалин и Бомбур выпивают 6 кувшинов компота за 330 мин, Бомбур и Глоин выпивают 3 кувшина за 330 мин, Глоин и Двалин — 2 кувшина за 330 мин.
=> 6>2+3 (если не брать в учет Глоина, для оценки)

Упростим лев. часть рав-ва:
cos2a\(1-sin2a)=(cos^2a-sin^2a)\(1-2sinacosa)=(cosa+sina)\(cosa-sina)
Упростим прав. часть:
(1+sina\cosa)\(1-sina\cosa)=(cosa+sina)(cosa-sina)
Видим, что данное рав-во яв-ся тождеством.