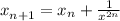

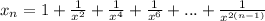
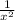
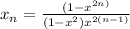
log(2) (4^x + 4) = x + log(2) (2^x*2^1 - 3)
log(2) (4^x + 4) = x + log(2) (2^(x+1) - 3)
ОДЗ
4^x + 4 > 0 x∈ R
2^(x+1) > 3
log(2) 2^(x+1) > log(2) 3
x + 1 > log(2) 3
x > log(2) 3 - 1 ≈ 1.59 - 1 ≈ 0.59
ОДЗ x ∈ (log(2) 3 - 1 , +∞ )
log(2) (4^x + 4) = x + log(2) (2^(x+1) - 3)
log(2) (4^x + 4) = log (2) 2^x + log(2) (2^(x+1) - 3)
log(2) (4^x + 4) = log(2) 2^x*(2*2^x - 3)
снимаем логарифмы
4^x + 4 = 2^x*(2*2^x - 3)
(2^x)^2 + 4 = 2*2^x*2^x - 3*2^x
(2^x)^2 - 3*2^x - 4 = 0
2^x = t > 0
t^2 - 3t - 4 = 0
D=9 + 16 = 25 = 5²
t₁₂ = (3 +- 5)/2 = -1 4
1. t₁ = -1
решений нет t>0
2. t=4
2^x = 4
x = 2 (входит в ОДЗ x > log(2) 3 - 1 )
ответ х=2
Скорость лодки 13км/ч, скорость течения 3км/ч.
Объяснение:
Пусть х-скорость лодки, а у-скорость течения.