9 класс Контрольная работа «Арифметическая и геометрическая прогрессии»
2 вариант
2. Найдите: а) пятый член арифметической прогрессии, если а1 = 8,
d1 = 2; б) четвертый член геометрической прогрессии, если b1т= 2.
3. В арифметической прогрессии (хn) известны х1 = 14 и х11 = 19.
Найдите номер члена прогрессии, равного 34 и сумму десяти
первых ее членов
4. В геометрической прогрессии разность четвертого и первого
членов равна 78, а сумма первых трех равна 39. Найдите первый
член прогрессии и её знаменатель.
РЕШИТЕ
СТАВЛЮ
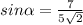 следовательно
следовательно 
( x + 2)²( (x + 2)² - 4) = 5
( x + 2)²( x² + 4x + 4 - 4) = 5
( x + 2)²( x² + 4x) = 5
(x² + 4x)(x² + 4x + 4) = 5
x⁴ + 4x³ + 4x² + 4x³ + 16x² + 16x - 5 = 0
x⁴ + 8x³ + 20x² +16x- 5 =0
Разложим на множители и решим:
(x² + 4x - 1)(x² + 4x + 5) = 0
Произведение равно 0,когда один из множителей равен 0,значит,
x² + 4x - 1 = 0
D = b² - 4ac = 16 - 4×(-1) = 20
x1 = ( - 4 + 2√5) / 2 = - 2(2 - √5)/2 = - (2 - √5) = √5 - 2
x2 = ( - 4 - 2√5)/2 = - 2( 2 + √5) / 2 = - ( 2 + √5) = - √5 - 2
x² + 4x + 5 = 0
D = b² - 4ac = 16 - 4×5 = - 4 - дискриминант отрицательный,значит,корней нет.
ответ: x1 = √5 - 2, x2 = - √5 - 2.