А) (1/3)*(1+1/2+1/4+1/8...)=1/3*(2⁰+2⁻¹+2⁻²)+...т.е. это сумма(1/3)/(2ⁿ⁻¹), где n меняется от 1 до ∞
Б) 1+1/3+1/9+1/27+...=сумма (1/3ⁿ⁻¹), где n меняется от 1 до ∞
В решении.
Объяснение:
Дана функция y=√x.
а) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
у=√х
1) А(0,04; 0,2)
0,2 = √0,04
0,2 = 0,2, проходит.
2) В(81; -9)
-9 = ±√81
-9 = -9, проходит.
3) С(54; 3√6)
3√6 = √54
3√6 = √9*6
3√6 = 3√6, проходит.
б) х∈ [0; 16]
y=√0 = 0;
y=√16 = 4;
При х∈ [0; 16] у∈ [0; 4].
в) у∈ [7; 13]
у = √х
7=√х х=7² х=49;
13=√х х=13² х=169.
При х∈ [49; 169] у∈ [7; 13].
Функция задана формулой f(x) = 2x² - 5x + 3
a)Найдите f(-1)
f(-1) = 2 * (-1)² - 5 * (-1) + 3 = 2 * 1 + 5 + 3 = 2 + 8 = 10
ответ: 10
б) Определите, при каких значениях X выполняется равенство f(x)=1
f(x)=1
2x² - 5x + 3 = 1
2x² - 5x + 2 = 0
D = b² - 4ac = 25 - 4 * 2 * 2 = 9
x₁ = (-b-√D)/2a = (5 - 3)/4 = 0,5
x₂ = (-b+√D)/2a = (5 + 3)/4 = 2
ответ: при x = 0,5 и x = 2.
в) Принадлежит ли графику функции точка A(1;0).
0 = 2 * 1² - 5 * 1 + 3
0 = 2 - 5 + 3
0 = 0
Значит, точка A(1;0) ∈ графику функции.
Функция задана формулой f(x) = 2x - 8
a) Определите, при каких значениях x f(x) > 0.
f(x) > 0
2x - 8 > 0
2x > 8
x > 4
При x ∈ (4; +∞) функция больше 0.
ответ: при x ∈ (4; +∞)
б) Найдите нули функции.
Нуль функции - место, где график функции пересекается с осью Ох. Приравняем к 0:
2x - 8 = 0
2x = 8
x = 4
ответ: 4
Найдите область определения функции:
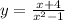
Найти область определения функции - значит найти значения, при которых функция имеет смысл.
Заметим, что если знаменатель будет равен нулю - функция бессмысленна. Тогда:
x² - 1 ≠ 0
x² ≠ 1
x ≠ ± 1
Область определения (ОДЗ): x ∈ ( - ∞; -1) ∪ (-1; 1) ∪ (1; + ∞).
Вольфрам подсказывает, что ответ похож на правду.