x+y=11
x-y=3
x=3+y
3+y+y=11
2y=11-3
2y=8
y=4
x=4+3
x=7
Числа = 7 и 4
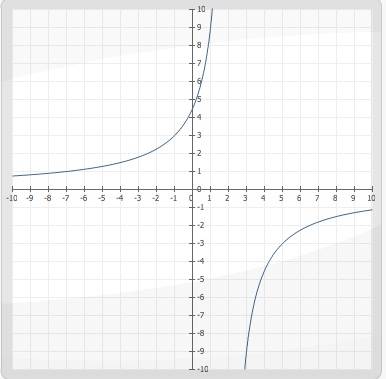
1. Для первого значения аргумента функция является непрерывной, т.к. подставляя значения аргумента в уравнение получим: 9/2 - это число, слудовательно, условие существования функции соблюдено. Для второго - разрывна, так как знаменатель оюращается в ноль, на ноль делить нельзя в школьной программе.
2. Из последнего предложение следует, что точка 2 - точка разрыва функции, тогда сможем найти лево- и правосторонние пределы: lim x to 2- = 9/ 0- = - бесконечность
lim х to 2+ = 9/0+ = + бесконечность
пусть будут два числа x y
x + y = 11
x - y =3
x + y + x - y = 11 +3
2x = 14
x = 7
7 + y = 11
y = 4
ответ 4 и 7