Можно решать несколькими :
1) метод сложения/вычитания двух уравненийНапример, дана система 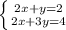 . Решим методом вычитания:
. Решим методом вычитания:
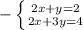
2x-2x + y-3y = 2-4
-2y = -2
y = 1
Далее это значение подставляется в любое из двух уравнений:
2х+1 = 2
2х = 1
х = 1/2
ответ: (1/2;1)
Метод сложения аналогичен этому методу, однако его лучше использовать, если в уравнении есть отрицательные значения
2) метод подстановкиЧтобы решить систему по этому методу, нужно выразить одну переменную из любого уравнения и подставить ее получившееся значение во второе уравнение системы
Пусть дана та же система 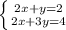 . Решим методом подстановки
. Решим методом подстановки
Выразим из первого уравнения у:
у = 2-2х
Подставим это вместо у во втором уравнении:
2х+3(2-2х)=4
2х + 6 - 6х = 4
-4х = -2
х = 1/2
Подставляем полученную точку в первое уравнение:
у = 2 - 2* 1/2
у = 1
ответ: (1/2; 1)
Важно! В ответе записывается точка в порядке (х;у)
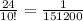

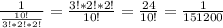
Объяснение:
Разберем подстановки на примере.
x + 5y = 7
3x − 2y = 4
Выразим из первого уравнения «x + 5y = 7» неизвестное «x».
Перенесём в первом уравнении «x + 5 y = 7» всё что содержит «x» в левую часть, а остальное в правую часть по правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
x = 7 − 5y
3x − 2y = 4
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
x = 7 − 5y
3(7 − 5y) − 2y = 4
Подставив вместо «x» выражение «(7 − 5y)» во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным «y». Решим его по правилам решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение «3(7 − 5y) − 2y = 4» отдельно. Вынесем его решение отдельно с обозначения звездочка (*).
x = 7 − 5y
3(7 − 5y) − 2y = 4 (*)
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1». Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение. Таким образом можно найти «x». Запишем в ответ оба полученных значения.
x = 7 − 5y
y = 1
x = 7 − 5 · 1
y = 1
x = 2
y = 1
ответ: x = 2; y = 1