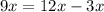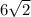 Объяснение:1 Запишем
Объяснение:1 Запишем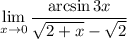 2 Умножим на 1
2 Умножим на 1Но мы представим 1 как дробь 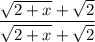 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
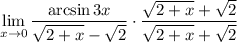
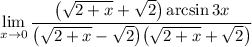
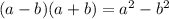 где
где
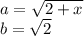
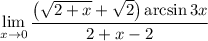
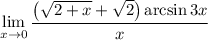
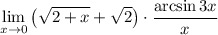 7 Представим предел произведения как произведение пределов
7 Представим предел произведения как произведение пределов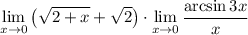 8 Посчитаем первый предел
8 Посчитаем первый предел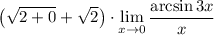
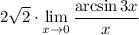 9 Так как
9 Так как 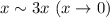 то мы можем заметить в пределе
то мы можем заметить в пределе  на
на 
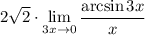 10 Умножим выражение пол пределом на 1
10 Умножим выражение пол пределом на 1Но 1 мы представим в виде 
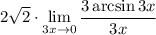
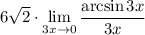
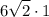 ОТВЕТ
ОТВЕТ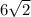
Примечание: