Пусть первоначальные вложения составляют х млн руб. (x∈N)
1 год : 100%+30%=130%; +30 млн руб
1,3x + 30 млн руб.
2 год : 100%+30%=130%; +30 млн руб
1,3(1,3x + 30) + 30 = 1,69x + 69 млн руб.
3 год : 100%+30%=130%; +15 млн руб
1,3(1,69x + 69) + 15 = 2,197x + 104,7 млн руб.
4 год : 100%+30%=130%; +15 млн руб
1,3(2,197x + 104,7) + 15 = 2,8561x + 151,11 млн руб.
Система неравенств по условию задачи
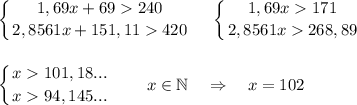
=====================================
Проверка :
1 год : 1,3 · 102 + 30 = 162,6 млн руб.
2 год : 1,3 · 162,6 + 30 = 241,38 млн руб > 240
3 год : 1,3 · 241,38 + 15 = 328,794 млн руб
4 год : 1,3 · 328,794 + 15 = 442,4322 млн руб > 420
ответ: 102 млн рублей
получаем ответ
[2;+ ∞)
Объяснение:
{1/x > 0, ⇒ x∈ (0;+ ∞)
{x2+3x–9 > 0 ⇒ x∈ (– ∞;–1,5–√10)U(–1,5+√10;+ ∞)
{x2+3x+(1/x)–10 > 0 ⇒x2+3x–10 > (–1/x)
см решение на рисунке
ОДЗ: x∈(b:+∞), b < 2
log3((1/x)·(x2+3x–9) ≤ log3(x2+3x+1/x–10)
Логарифмическая функция с основанием 3 > 1 монотонно возрастает.
(1/х)·(x2+3x–9) ≤ x2+3x+(1/x) –10;
(1/х)·(x2+3x–9) –x2–3x–(1/x)+10 ≤ 0;
(1/х)·(x2+3x–9–1)–(x2+3x–10) ≤ 0;
(x2+3x–10)·((1/x)–1) ≤ 0;
(x–2)(x+5)(1–x)/x ≤ 0.