1). Второе слагаемое умножается и делится на 2. В результате получается удвоенное произведение b/2a и х.
Так как квадрат х представлен в качестве первого слагаемого, то для полного квадрата суммы не хватает квадрата второго слагаемого, то есть (b/2a)².
Добавляем этот недостающий элемент и, чтобы значение выражения не изменилось, - вычитаем его же.
c/a оставляем без изменений:
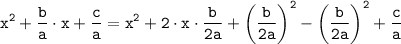
2). Записываем получившийся полный квадрат суммы:
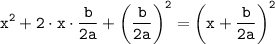
Оставшиеся два слагаемых группируем со сменой знака:
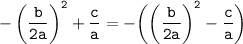
Приводим выражение в скобках к общему знаменателю 4а²:
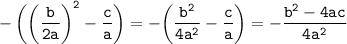
3). Получаем в результате:

Чтобы А³ была нулевой матрицей, но чтобы при этом матрица А² не была нулевой, нужно чтобы в матрице А² все элементы кроме одного были равны нулю. Тогда в матрице А должны быть все элементы кроме двух равны нулю. Таким условиям отвечает, матрица, в которой, например два элемента находящихся на линии, параллельной главной диагонали, равны 1, а все остальные элементы матрицы равны нулю:
Или:
Тогда при возведении первой матрицы в квадрат получим матрицу:
А при возведении второй матрицы в квадрат получим:
А возведя в третью степень обе матрицы, получим нулевые матрицы.
ответ: