Решите уравнение. |x^2-3|x|-2|=2
Объяснение:
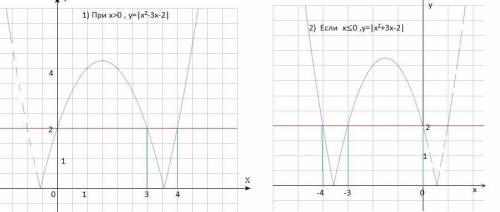
1) Пусть х>0 , тогда |x²-3x-2|=2.
Построим у= |x²-3x-2| и у=2. Найдем точки пересечения графиков
а) у= |x²-3x-2| парабола с отображенной частью относительно оу, находящейся ниже оси ох. Строим по точкам, затем отображаем:
х 0 0,5 1 1,5 2 3
у 2 3,25 4 4,25 4 2.
у=2 прямая , параллельная оси ох.
Точки пересечения х=3,х=4.
2) Пусть х≤0 , тогда |x²+3x-2|=2.
Построим у= |x²+3x-2| и у=2. Найдем точки пересечения графиков
а) у= |x²+3x-2| ,парабола с отображенной частью относительно оу, находящейся ниже оси ох. Строим по точкам, затем отображаем:
х -4 -3 -2 -1 0
у 2 2 4 4 2
у=2 прямая , параллельная оси ох.
Точки пересечения х=-4,х=-3 ,х=0
ответ :-4;-3;0;3;4.
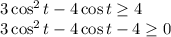
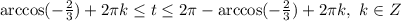
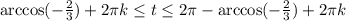 , где k - целые числа
, где k - целые числа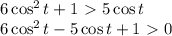
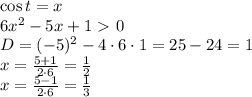
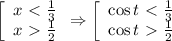
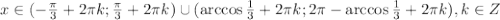
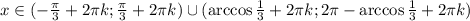 , где k - целые числа
, где k - целые числа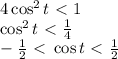
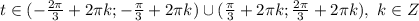
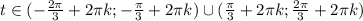 , где k - целые числа
, где k - целые числа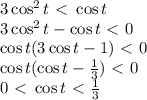

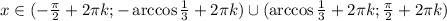 , где k - целые числа
, где k - целые числа
1) 3x^2-2*(x-1)-10=0 x>=1 3x^2-2x-8=0 x=(1+-5)/3 x=2 x=-4/3 x=2 x<1 3x^2+2x-2-10=0 3x^2+2x -12=0 x=(-1+sqrt(37))/3 2) x>=2 5x^2-4x+8-14<=0 5x^2-4x-6<=0 нет
решения x<2 5x^2+4x-8-14<=0 x<2 5x^2+4x-22<=0 (-2+-sqrt(114))/5 [(-2-sqrt(114))/5;2]
3) x^2-2x-15>x^2-135 2x<120 x<60 x<=-3 U x>=5 x<=-3 U [5;60) (-3;5) -x^2+2x+15>x^2-135 2x^2-2x-150<0 x^2-x-75<0 (1-sqrt(301)/2;1+sqrt(301)/2) (-3;5) ответ:x<60