Биномиальное распределение стремится к нормальному при больших n
По условию
р = 0.9
соответственно
q = 1- p = 0.1
Математическое ожидание
М= np= 1000 * 0.9 = 900
Дисперсия
D= npq = 1000*0.9*0.1= 90
Сигма = √D= 3√10 = ~9.5
Мы рассматриваем интервал от центра распределения 900 до 940 - это больше чем четыре сигмы.
В этом случае в табличку нормального распределения можно даже не заглядывать, хвостик за четыремя сигмами очень малюсенький, пятый знак после запятой.
Половина всей выборки до 900 , половина после.
ответ
Вероятность равна ~0.5
Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: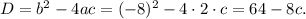 
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: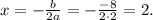 
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: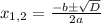 
. Выразим каждый из корней:
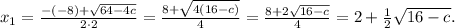
Аналогично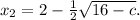 
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: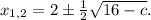 
ОТВЕТ: если с < 8, то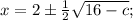 
если с = 8, то х = 2; если с > 8, то корней нет.
ответ А. 5; 6.
Объяснение: