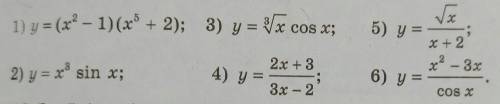
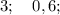
Объяснение:
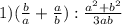
1. Сначала выполним сложение в скобках. Общий знаменатель двух дробей:
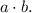
Дополнительный множитель для первой дроби:
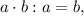
Дополнительный множитель для второй дроби:

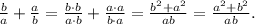
2. Деление на дробь равносильно умножению на обратную дробь:
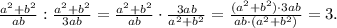
ответ: 3.
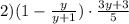
1. Сначала выполним вычитание в скобках. Единицу представим как дробь со знаменателем 1:
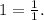
Общий знаменатель двух дробей:
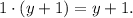
Дополнительный множитель для первой дроби:
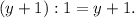
Дополнительный множитель для второй дроби:
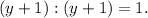
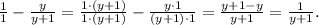
2. Вынесем тройку за скобки в числителе второй дроби:
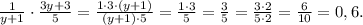
ответ: 0,6.
А) Точки пересечения с осями : (0, -2) и (5,0).
Б) Точка не принадлежит графику.
Объяснение:
А)
Функция х - 2,5 у - 5=0. имеет неприведенный вид. Для начала выразим у:
у = 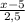
Пересечение с осями определяется приравниванием х и у к нулю:
Если х = 0, то у = -2 график пересекает ось у
Если у = 0, то х = 5 график пересекает ось х
Точки пересечения с осями : (0, -2) и (5,0)
Б)
Чтобы проверить, принадлежит ли точка графику функции подставим вместо х --> -5,5 , а вместо у --> -2,6
-2,6 = 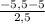 выражение неверно , а значит точка не принадлежит графику.
выражение неверно , а значит точка не принадлежит графику.
1.
2.
3.
4.
5.
6.