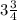В прямоугольном треугольнике высота, длиной 12 см, проведенная к гипотенузе, делит ее на отрезки, разница между которыми равна 7 см. Найдите периметр.
Пусть отрезки равны х и у и x>y по условию x-y=7 Высота через отрезки равна H^2=xy Решим систему {xy=144 {x-y=7
{x=7+y {7y+y^2=144
y^2+7y-144=0 y=9 x=16 Значит отрезки равны 16 и 9 , а вся гипотенуза равна 16+9 = 25, Теперь найдем катеты через известное соотношение H=ab/c где а и в катеты и теорема пифагора a^2+b^2=25^2 {ab/25=12 {a^2+b^2=625
решая получим a=15 . b =20 И того периметр равен P=20+15+25 = 60
-2 -1 1 3 Отмечаем на числовой прямой точки х_1 х_2 х_3 х_4 и т. д. Справа пишем функции и отмечаем знаки функций. А затем выбираем нужные интервалы. В данном неравенстве решением будет. (-2; -1) объединение (1; 3)
(2x+3y)/4=(3x+4y)/7,
(5y-6x)/10=(-4x+12)/2;
из первого уравнения:
(2x+3y)/4=(3x+4y)/7
(2x+3y)/4-(3x+4y)/7=0
7(2x+3y)-4(3x+4y)=0
14x+21y-12x-16y=0
2x+5y=0
2x=5y
x=y*5/2
упростим второе уравнение:
(5y-6x)/10=(-4x+12)/2
(5y-6x)/10-(-4x+12)/2=0
5y-6x+20x-60=0
5y+14x=60
Подставим x=y*5/2
5y+14y*5/2=60
5y+35y=60
40y=60
y=60/40=3/2=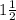
x=y*5/2=3/2*5/2=15/4=