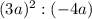Найдите его значение, если a = -8
Имеются пятизначные слагаемые. Если в каждом пятизначном числе убрать по две цифры, мы получим сумму трёх трёхзначных чисел. Чтобы сумма полученных трёхзначных чисел была наибольшая, необходимо, чтобы каждое число было наибольшим из возможных. А для этого нужно, чтобы число сотен, десятков и единиц в каждом числе было наибольшим.
Так, в первом числа 95571 убираем цифры 5 и 1, получаем 957. Это наибольшее из всех трёхзначных чисел, которое можно получить из данного пятизначного числа.
Подобным образом из числа 49134 убираем первую цифру 4 и цифру 1, получаем число 934.
Их числа 23627 убираем первую двойку и цифру 3. Получаем число 627.
Итак, полученная сумма 957+934+627=2518 будет наибольшей из возможных.
ответ: 2518 - наибольшая сумма
Объяснение:
Основное свойство дроби:
если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
1) Умножаем числитель и знаменатель на (-1):
А/В = А*(-1) /В *(-1) = (-А)/(-В)
2) То же самое и со второй дробью:
(-А)/В = (-А)*(-1) /В *(-1) = А/(-В)
При записи отрицательных дробей знак "минус", который стоит перед числителем или перед знаменателем, можно ставить перед дробью, т.е.
(-А)/В = А/(-В) = - А/В
(-3)/2 = (-3) * (-1) /2*(-1) = 3 / (-2) = -3/2
(-3)/2 = -3/2
(-4)/(-5) = 4/5
Т.е. если знаки разные в числителе и знаменателе, то минус можно поставить перед всей дробью.
Если знаки одинаковые ( +/+ или - / -), то знак общей дроби будет плюс.
Объяснение: