Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
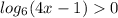решаем данное неравенство.
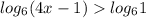
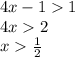
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
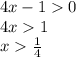
рассматриваем оба неравенства и находим область пересечения интервалов
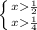x∈ [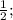 
+∞ [
7. 
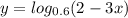значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
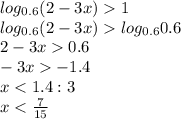
находим область пересечения обоих условий,
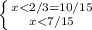x∈ ] -∞; 7/15 [
8. 
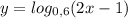область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
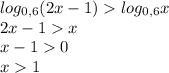
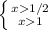x∈ ] 1; +∞ [
2t^2+t-1=0
t1=(-1-3)/4=-1
t2=(-1+3)/4=1/2
Вернёмся к замене
sinx=-1
x=-Π/2+2Πn, n€Z
sinx=1/2
x1=Π/6+2Πm, m€Z
x2=5Π/6+2Πm, m€Z
ответ: -Π/2+2Πn, n€Z; Π/6+2Πm, 5Π/6+2Πm, m€Z
2) 6cos^2x+cosx-1=0
Пусть t=cosx, где t€[-1;1], тогда
6t^2+t-1=0
t1=(-1-5)/12=-1/2
t2=(-1+5)/12=1/3
Вернёмся к замене:
cosx=-1/2
x=+-arccos(-1/2)+2Πn, n€Z
cosx=1/3
x=+-arccos(1/3)+2Πm, m€Z
ответ: +-arccos(-1/2)+2Πn, n€Z; +-arccos(1/3)+2Πm, m€Z
3) 2cos^2x+sinx+1=0
2(1-sin^2x)+sinx+1=0
-2sin^2x+sinx+3=0
Пусть t=sinx, где t€[-1;1], тогда
-2t^2+t+3=0
t1=(-1-5)/-4=-1,5 посторонний, т.к. t€[-1;1]
t2=(-1+5)/-4=-1
Вернёмся к замене
sinx=-1
x=Π/2+2Πn, n€Z
ответ: Π/2+2Πn, n€Z