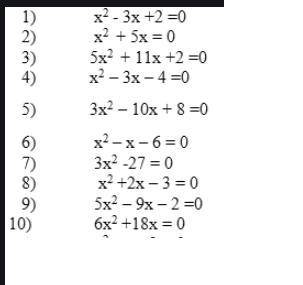
1) 5х^4
2)1/x^2 - 3
3)16x^3 = 1/(2sqrt(x)) sqrt(x) - эт корень из x
4)x^2 - 1/sqrt(x) - 5/x^2
5)(5x-4)'(2x^4 - 7x + 1) + (5x-4)(2x^4 - 7x + 1)' =
= 5(2x^4 - 7x + 1) + (5x-4)(8x^3 - 7)=
= 10x^4 - 35x +5 +40x^4 - 35x - 32x^3 + 28
= 50x^4 - 32x^3 - 70x + 28
6)((x^3-7)'(3-4x^4) - (x^3 -7)(3-4x^4)')/(3-4x^4)^2 =
= (3x^2*(3-4x^4) + 16x^3*(x^3 - 7))/(3-4x^4)^2 =
= (9x^2 - 12x^6 + 16x^6 - 112x^3)/(4x^4-3)^2 =
= (4x^6 - 112x^3 +9x^2)/(16x^8 - 12x^4 - 9)
7)16 * 1/4 * (x/4 +6)^16 = 4(x/4 +6)^16
8)3sin(5-3x)
9)0.5 * 1/(2sqrt(42+0,5x)) = 1/(4sqrt(42+0,5x))
Найдите первообразную F(x) для функции f(x) = 2 + sin4x ,
если F(π/4) = -3π . В ответе укажите F(7π/4) .
F(x) = ∫f(x)dx =∫( 2 + sin4x)dx =∫2dx + ∫sin4xdx =∫2dx +(1/4)∫sin4xd(4x) =
= 2x - cos(4x) / 4 + C .
F(x) = 2x - 0,25cos(4x) + C ( семейство первообразных ) Определим постоянной С используя условие : F(π/4) = - 3π
F(π/4) =2*π/4 - 0,25cos(4*π/4) +C=0,5π +0,25cos(π) + C
- 3π = 0,5π + 0,25 + C ⇒ C = - 3,5π - 0,25
F(x) = 2x - 0,25cos(4x) - 3,5π - 0,25 .
F(7π/4) = 2*(7π/4) - 0,25cos(4*(7π/4)) - 3,5π - 0,25 =
= 3,5π - 0,25cos(7π) - 3,5π - 0,25 = 0
ответ: 0
* * * P.S. F(7π/4) можно получить другим
F(7π/4) - F(π/4) = 2*(7π/4) - 0,25cos(4*(7π/4)) - 2*π/4 + 0,25cos(4*(π/4)) = 3,5π - 0,25cos(7π) - 0,5π + 0,25cos(π) =3π
F(7π/4) = F(π/4) + 3π = - 3π + 3π = 0
ответ: 1) 1;2
2)0;-5
3) - 2; - 0,2
4) -1;4
5) 1 1/3; 2
6) - 2;3
7) 3;-3
8)-3;1
9)7; 9,2
10) 0;-3
Объяснение:
1) По виету
x1+x2=3
x1*x2=2
Значит x1=1, x2=2
2) Выносим x
x(x+5)=0
Значит x1=0, x2=-5
3) Через дискримант
D=121-40=81
x1=(-11-9)/10=-2
x2=(-11+9)/10=-0,2
4) Через виета
x1+x2=3
x1*x2=-4
Значит x1=-1,x2=4
5) через дискримант
D=100-96=4
x1=(10-2)/6=1 1/3
x2=(10+2)/6=2
6)Через виета
x1+x2=1
x1*x2=-6
Значит x1=-2,x2=3
7)Выносим 3
3(x2-9)=0
x^2=9
x1=3,x2 =-3
8) Через виета
x1+x2=-2
x1*x2=-3
Значит x1=-3,x2=1
9)Через дискриминант
D=81+40=121
x1=(81-11)/10=7
x2=(81+11)/10=9,2
10) Выносим 6x
6x(x+3)=0
x=0,x=-3