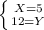
Думаю, такие задачи проще всего решать в виде системы уравнений.
Составим систему.
Примем за скорость пешехода X, а за скорость велосипедиста Y. И из первого предложения задачи можем составить первое уравнение:
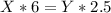
А из второго предложения, второе уравнение:
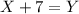
Итого получаем систему из двух уравнений с двумя неизвестными:
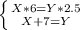
В нашем случае мы получили во втором уравнении сразу то, что надо - выражение Y через X и мы можем сразу подставить его в первое уравнение:
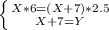
Раскрываем скобки в первом уравнении и переносим все X в левую часть уравнения и решаем его.
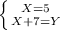
В общем, мы уже нашли ответ, так как в задаче спрашивалась только скорость пешехода и мы нашли, что она равна 5км*ч (похоже на правду). Но можно и решить систему полностью, то есть, найти еще и скорость велосипедиста. Для этого подставляем полученное значение X во второе уравнение и получаем ответ:
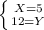
Думаю, такие задачи проще всего решать в виде системы уравнений.
Составим систему.
Примем за скорость пешехода X, а за скорость велосипедиста Y. И из первого предложения задачи можем составить первое уравнение:
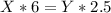
А из второго предложения, второе уравнение:
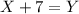
Итого получаем систему из двух уравнений с двумя неизвестными:
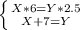
В нашем случае мы получили во втором уравнении сразу то, что надо - выражение Y через X и мы можем сразу подставить его в первое уравнение:
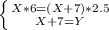
Раскрываем скобки в первом уравнении и переносим все X в левую часть уравнения и решаем его.
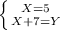
В общем, мы уже нашли ответ, так как в задаче спрашивалась только скорость пешехода и мы нашли, что она равна 5км*ч (похоже на правду). Но можно и решить систему полностью, то есть, найти еще и скорость велосипедиста. Для этого подставляем полученное значение X во второе уравнение и получаем ответ: