
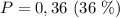
Объяснение:
Решим задачу через геометрическое определение вероятности.
Обозначим за х и у время прихода пассажиров:
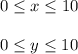
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата. Пассажиры встретятся, если между моментами их прихода пройдет не более 2 минут, то есть:
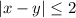
Что равносильно следующей системе:
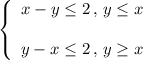
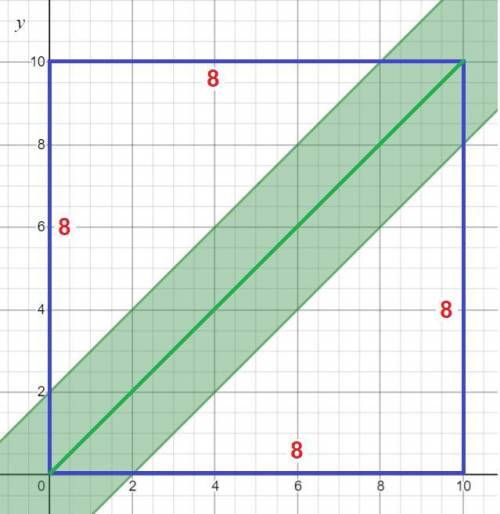
На графике такая область выглядит следующим образом (см. рисунок).
Тогда вероятность встречи равна отношению площади закрашенной области к площади всего квадрата.
Площадь закрашенной области равна разности площади квадрата и двух прямоугольных треугольников с катетами 10-2=8 .
Тогда:
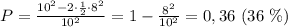
если даже разложить квадрат разности по формуле сокращенного умножения:
(4х-4у)² = (16x²-2*4x*4y+16y²) = (16x²-32ху +16у²) = 16(х²-2ху +у²) =
= 16 (х-у)²
2) (5у+5)²= (5(y+1))²= 25 (у+1)²
или
(5у+5)²= (25у²+2*5*5у +25) = 25(у²+2у+1) = 25*(у+1)²
3) (8m-10n)³ = (2*4m -2*5n)³= 8(4m-5n)³
4) (a²-9a)² = (a (a-9))²= a² (a-9)²
5) (6x-9y)³= (3 (2x-3y))³= 27 (2x-3y)³
6)(22x⁴-28x⁴-28x²y³) ⁵ = (-6x⁴-28x²y³) ⁵=
= (2x² (-3x²-14y³))⁵=
= 2⁵x⁵*² (-3x²-14y³)⁵ = 32x¹⁰ (-3x²-14y³)⁵
или
= (-2х² (3х² +14у³))⁵ = -32х¹⁰ (3х²+14у³)⁵