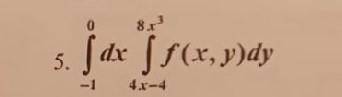
1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)
Построение графика функции методом дифференциального исчисления
Математика онлайн Математический анализ
1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.
y(-x)=
Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
x=0, y=
Пересечение с осью 0X
y=0
3·x4+4·x3+1=0
Нет пересечений.
5) Исследование на экстремум.
y = 3*x^4+4*x^3+1
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 12·x3+12·x2
или
f'(x)=12·x2·(x+1)
Находим нули функции. Для этого приравниваем производную к нулю
x2·(x+1) = 0
Откуда:
x1 = 0
x2 = -1
Обратимся к рисунку. Видим, что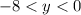 .
.
Причём, пока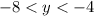 , переменная
, переменная  меняется от
меняется от ![x=\dfrac{\sqrt[3]{y}}{2}](/tpl/images/1855/6786/5969b.png) до
до 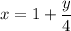 .
.
Когда же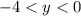 , то
, то  меняется от
меняется от ![x=\dfrac{\sqrt[3]{y}}{2}](/tpl/images/1855/6786/5969b.png) до
до 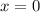 .
.
Таким образом,