 функция
функция 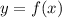 не существует. То есть найдем такие значения
не существует. То есть найдем такие значения  , при которых выражение
, при которых выражение 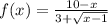 не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла: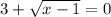 , однако понятно, что
, однако понятно, что 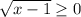 , значит знаменатель не обратиться в нуль.
, значит знаменатель не обратиться в нуль.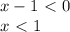
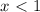 функции не существует. То есть она идет от
функции не существует. То есть она идет от  и куда-то дальше. Куда — нам пока неизвестно.
и куда-то дальше. Куда — нам пока неизвестно.  . Может быть она периодична?
. Может быть она периодична? 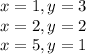
 , при котором числитель обратиться в нуль.
, при котором числитель обратиться в нуль. 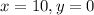
 повставлять разные значения (большие и маленькие).
повставлять разные значения (большие и маленькие). 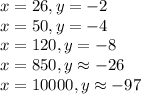
 уменьшается
уменьшается 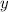 . Делаем вывод, что функция убывает бесконечно много. То есть
. Делаем вывод, что функция убывает бесконечно много. То есть 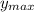 — не существует,
— не существует, 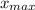 — не существует.
— не существует. 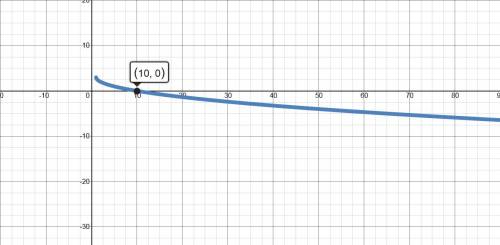
|x| = -x при х <0
Придётся определять какое число стоит под знаком модуля, чтобы потом этот самый знак снять.
каждое подмодульное выражение = 0 при х = -2, 3, 2
Поставим эти числа на координатной прямой
-∞ -2 2 3 +∞
Получили 4 промежутка. на каждом отдельно будет уравнение иметь свой вид
а) (-∞; -2)
-(х+2) +(х-3) +(х-2) = 3
-х-2+х-3+х-2 = 3
х = 10 ( в указанный промежуток не входит)
б)[-2; 2)
х+2 +х -3 +х-2 = 3
3х = 6
х = 2 ( в указанный промежуток не входит)
в) [2; 3)
х +2 +х -3 -х -2 = 3
х =6 ( в указанный промежуток не входит)
г)[3; +∞)
х +2 -х+3 -х+2 = 3
-х = -4
х = 4 ( в указанный промежуток входит)
ответ: 4