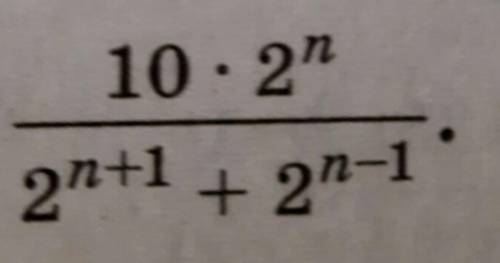
Объяснение:
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
бум бум бум бум юуи.ювьвлчжты
К трем задачам по готовым рисункам заданы одинаковые вопросы. 1)Докажите, что ∆ АВС=∆ADC. 2) Является ли биссектрисой угла ВСD луч СА? (рис.1,3) 3) Докажите, что ∆ ВСF=∆ DCF (рис.1,3)
Рис.1 В четырехугольнике АВСD диагонали АС и ВD пересекаются в т.F под прямым углом. АВ=АD; угол ВАD=DАF.
1) В треугольнике ВАD стороны AB=AD ⇒ он равнобедренный; АF делит угол А поровну ( дано) ⇒AF– биссектриса и высота. Т.к. ∆ ВАD равнобедренный, то АF медиана. ВF=DF, угол BFC=90° ⇒ FC - медиана и высота треугольника ВСD, это признак равнобедренного треугольника, из чего следует СВ=СD. В ∆ АВС и ∆ ADC стороны АВ=AD; BC=DC, АС - общая. Эти треугольники равны по трем сторонам, т.е. по 3-му признаку равенства.
2) АС – медиана и высота равнобедренного треугольника, значит, и биссектриса его угла.
3) Из доказанного выше СВ=CD, BF=DF, СF общая, АС - биссектриса. ∆ ВСF=∆ DCF по 1-му признаку ( две стороны у угол между ними) и 3-м сторонам ( по 3-му признаку).
Рис.2. В четырехугольнике АВСD диагональ АС при пересечении двух противоположных сторон образует равные накрестлежащие углы САD=ACD=60°. => Если накрестлежащие углы при пересечении двух прямых секущей равны, эти прямые параллельны. => угол АСD=углу ВАС=30°. ∆ АВС=∆ АСD по стороне двум равным углам, прилежащим к ней (2-й признак равенства).
Рис.3. Диагональ АС четырехугольника АВСD делит его на треугольники со сторонами АВ=AD; CD=CB, АС - общая.
1) ∆ АВС и ADC равны по трем сторонам (3-й признак равенства).
2) Из п.1. следует < BCA= < DCA => АС - биссектриса угла ВС D.
3) В ∆ BCF и ∆ DCF стороны ВС=DC (дано), углы при вершине С равны (доказано), CF- общая. Эти треугольники равны по двум сторонам и углу между ними, т.е. по 1-му признаку равенства треугольников.
Объяснение:
(10*2^n)/(2^(n+1)+2^(n-1);
(10*2^n)/(2^n*2^1)+2^n*2^(-1));
(10*2^n)/2^n*(2+2^(-1));
2^(-1)=1/2, (10*2^n)/2^n*(2+1/2);
(10*2^n)/2^n*(5/2);
Разделим 10*2^n на 2^n*(5/2), 10/(5/2) ;
Разделим 10 на 5/2, получим: 20/5=4 ;
ответ: (10*2^n)/(2^(n+1)+2^(n-1) =4.