напр. (1/3;1/4); (1/9; 5/12); (1/27; 53/36)
3х+4у=2
y=(2-3x)/4 (*)
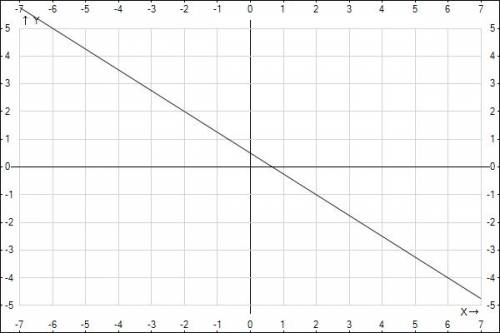
из графика видно, что при 0<x<0.5 (а еще точнее при 0<x<2/3=0.(6)) у точки абсциса и ордината будут иметь одинаковые (положительные) знаки(x>0, y>0)
взяв любые три значения переменной х в указанном интервале
1/3 или 1.9 или 1.27
или 0.1 или 0.2 или 0.3 и т.д. и посчитав соотвествующее значения y для х по формуле (*) находим точки
напр. еще три точки
x=0.1 y=(2-3*0.1)/4=0.25*(2-0.3)=0.25*1.7=0.425
получаем точку (0.1; 0.425)
x=0.2 y=(2-3*0.2)/4=0.35
(0.2; 0.35)
x=0.3 y=(2-3*0.3)/4=0.275
(0.3; 0.275)
Пусть это число А, так как оно окончивается цифрами 17 и делится на 17 (17 делится на 17), то представив число А в виде A=100B+17, где B - некоторое неотрицательное целое число. Видим что A-17=100B+17-17=100B должно делится на 17, так как 100 на 17 не делится, то число В должно делится на 17. При данных условиях оно должно быть наименьшим, и сумма цифр должна ровнять 17-1-7=9
Так как сумма цифр числа В равна 9, то оно делится на 9(а так как оно делится еще на 17), НОК(9, 17)=9*17=153, значит число В равно 153, а данное число равно
15317