Решение системы уравнений (1; -3).
Объяснение:
Решите методом сложения систему уравнений:
7x-y=10
5x+y=2
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе ничего преобразовывать не нужно, коэффициенты при у одинаковые и с противоположными знаками.
Складываем уравнения:
7х+5х-у+у=10+2
12х=12
х=1
Подставим значение х в любое из двух уравнений системы и вычислим у:
7x-y=10
-у=10-7х
у=7х-10
у=7*1-10
у= -3
Решение системы уравнений (1; -3)
Объяснение:
Периметр - сумма длин всех сторон:
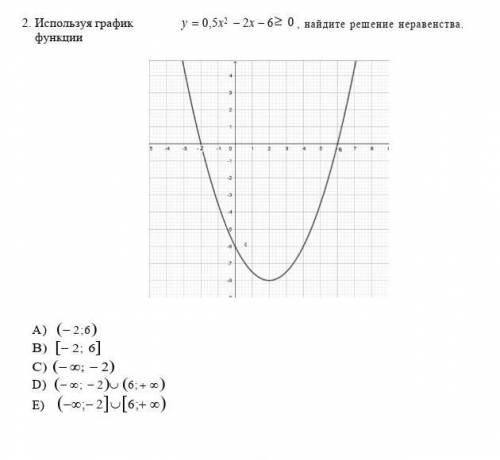
Р=(-1-2b)+(-2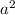 b-
b-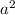 )+(3a+6ab).
)+(3a+6ab).
Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
В нашем случае нужно раскрыть скобки и привести подобные слагаемые:
-1-2b+-2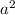 b-
b-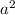 +3a+6ab - подобных слагаемых нет. Располагаем все эти слагаемые в порядке понижения степени:
+3a+6ab - подобных слагаемых нет. Располагаем все эти слагаемые в порядке понижения степени:
2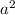 b-
b-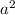 +6ab+3a-2b-1.
+6ab+3a-2b-1.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов; в нашем случае - наибольшая степень - это 2.
Как это теперь записать:
Р=(-1-2b)+(-2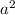 b-
b-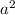 )+(3a+6ab)=-1-2b+-2
)+(3a+6ab)=-1-2b+-2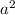 b-
b-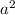 +3a+6ab=2
+3a+6ab=2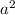 b-
b-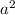 +6ab+3a-2b-1; степень многочлена - 2.
+6ab+3a-2b-1; степень многочлена - 2.
X= 1-2-5-6+%:+')167% вот