Решение Половина пути для второго автомобиля 0,5. Пусть х км/ч – скорость первого автомобилиста, тогда (х + 54) км/ч - скорость второго автомобилиста Время второго автомобиля, за которое он весь путь 0,5 / 36 + 0,5/(x + 54) Время первого автомобиля равно времени второго автомобиля. 1/x = 0,5 / 36 + 0,5/(x + 54) 1/x - 0,5 / 36 - 0,5/(x + 54) = 0 36(x + 54) – 0,5x(x + 54) – 0,5*36x = 0 36x + 1944 – 0,5x² - 27x – 18x = 0 – 0,5x² - 9x + 1944 = 0 I : (-0.5) x² + 18x – 3888 = 0 D = 324 + 4*1*3888 = 15876 = 1262 X₁ = (- 18 – 126)/2 = - 72 не удовлетворяет условию задачи X₂ = (- 18 + 126)/2 = 54 54 км/ч - скорость первого автомобилиста ответ: 54 км/ч
6. -5 ≤ А ≤ 35
ответ 4).
7.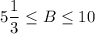
ответ 1)
Объяснение:
Требуется оценить выражение.
6.
-4 ≤ a ≤ 1; A = 3 - 8a
Если обе части неравенства умножить или разделить на отрицательное число, знак неравенства перевернется.Умножим все части неравенства на (-8), перевернув знаки неравенства:
-4 ≤ a ≤ 1 | · (-8)
32 ≥ -8a ≥ -8
или
-8 ≤ -8а ≤ 32
Если ко всем частям неравенства прибавить или отнять одно и то же число, то получим неравенство, равносильное данному.Прибавим ко всем частям неравенства 3:
3 - 8 ≤ 3 - 8а ≤ 3 + 32
-5 ≤ 3 - 8а ≤ 35
-5 ≤ А ≤ 35
ответ 4).
7.
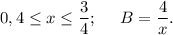
Если a и b - положительные числа и а > b, то 1/а < 1/b.Переведем 0,4 в обыкновенную дробь.
Перевернем наши дроби, при этом знак неравенства тоже перевернется:
Умножим все части неравенства на 4:
ответ 1)