
Объяснение:
Пусть скорость пешехода - х км/час
а скорость велосипедиста - y км/час
Длина пути от города до деревни : 30 км
1) Велосипедист выехал на 45 мин позже пешехода и был в пути 30 мин.
30 мин = 30/60 = 0,5 часа
Расстояние , которое проехал велосипедист составило : 0,5y км
Пешеход был в пути :
45 мин +30 мин= 75 мин
75 мин = 75/60= 1,25 часа
Расстояние , которое пешеход составило : 1,25х км
Велосипедист был позади пешехода на 2,5 км , значит можем составить первое уравнение :
1,25x -0,5y= 2,5 (1)
2) Велосипедист ехал еще 30 мин , значит общее время составило :
30 мин +30 мин = 1 час , а расстояние , которое он преодолел было :
1*y км
Время движения пешехода было : 75 мин. +30 мин= 105 мин
105 мин = 105/60= 1,75 часа, расстояние он преодолел : 1,75x км
При этом велосипедист был на 0,5 км от деревни дальше , чем пешеход . Можем составить второе уравнение:
1,75х - y =0,5 ( 2)
Получаем систему уравнений :
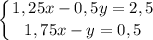
Домножим первое уравнение на 2
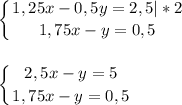
отнимем от первого уравнения второе
0,75х= 4,5
х= 4,5 : 0,75
х= 6 км/час - скорость пешехода
подставим значение х в любое уравнение и найдем y
2,5*6-y= 5
15-y= 5
y= 15-5=10 км/час - скорость велосипедиста
ответ:4 км/ч
Объяснение:
Пусть первоначальная скорость поезда будет х км/ч,тогда увеличенная скорость будет х+1 км/ч. Первоначальное запланированное время в пути тогда будет 60/х часов,а ускоренное время будет 60/х+1 часов.Разница между первоначальным и ускоренным временем в пути составляет 3 часа.Составляем уравнение: 60/х - 60/х+1 =3. Решаем: 60(х+1) - 60*х=3(х^2+х) 60х+60-60х=3х^2+3х 3х^2+3х-60=0 D=3^2-4*3*(-60)= 9+720=729 x1= (-3-27 )/2*3=-30/6=-5; х2=(-3+27)/2*3=24/6=4. х1 имеет отрицательное значение,а значит не удовлетворяет условию задачи - скорость поезда не может быть отрицательной ,а х2 положительное число,значит удовлетворяет условию задачи.Следовательно,первоначальная запланированная скорость поезда составляла 4 км/ч.