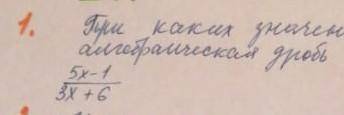
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы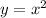 
путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒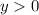 
при 
.
Пр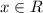есечение с осью ОУ в точке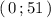 
.
Убывает при ![x\in (-\infty ;\, 5\ ]](/tpl/images/1657/0857/c774b.png)
, возрастает при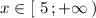 
.
Точка минимума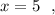 
минимальное значение функции 
.
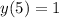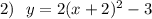
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика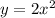 
вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
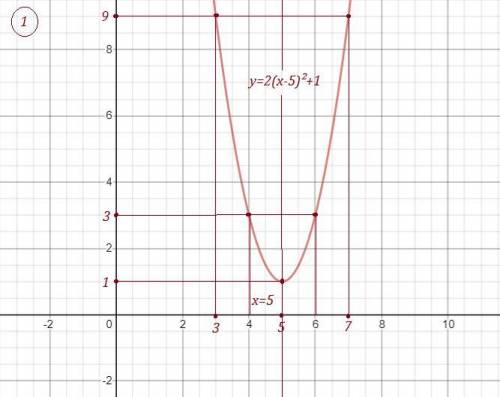
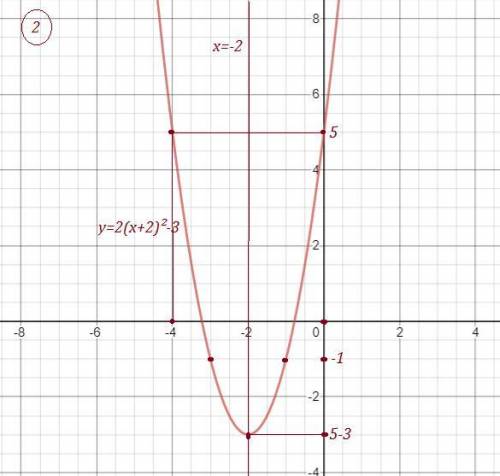
Все функции - параболы вида
a - определяет "ширину" ветвей, при 0<а<1 ветви "шире", при а > 1 "уже"
При отрицательном а - ветви направлены вниз, при положительном вверх. В 3 и 4 примерах а = -1, поэтому ветки вниз
b - (в данных примерах не используется) показывает смещение вершины параболы вдоль оси OX, положительный левее, отрицательный правее от оси OY
с - смещение вершины графика вдоль оси OY - положительный с - выше, отрицательный ниже, при с=0 ветка графика пересекает точку 0,0
Объяснение:
x ≠ -2, т.е. при любом x, не равном -2.
Объяснение:
Не имеет смысл дробь только когда знаменатель = 0, т.е.: