
Пусть х минут - то время, за которое можно наполнить чан через кран А, тогда через кран В чан заполняется за (х-11) минут. За 1 минуту: через кран А наполняется 1/х чана, через кран В - 1/(х-11) чана, через кран А и кран В 1/х+1/(х-11) или 1/30 чана. Составим и решим уравнение:
1/х+1/(х-11)=1/30 |*30x(x-11)
30x-330+30x=x^2-11x
x^2-11x-60x+330=0
x^2-71x+330=0
по теореме Виета:
х1=66 х2=5 (не подходит, так как х-11 не может быть отрицательным числом)
66 мин.=1 ч. 6 мин.
ответ: через кран А чан может наполниться за 1 час 6 минут.
1)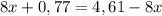
____________________________________________________
1,92+0,77=4,61-1,92
2,69=2,69
======================================================
2)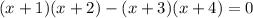
_______________________________________________________
=======================================================
3)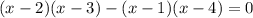
корней нет
=======================================================
4)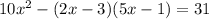
_______________________________________________________
========================================================
5)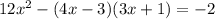
___________________________________________________________