Данная функция является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию:
Для нахождения единственного экстремума воспользуемся производной:
По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением .
Для нахождения точки экстремума вычислим значение исходной функции от найденного :
Примем: Х км/час скорость по шоссе; 32/Х время по шоссе; (Х+20) скорость по автостраде; 60/(Х+20) время по автостраде. Так как общее время = 1 час, составим и решим уравнение: 32/Х + 60/(Х+20) = 1; приведем к общему знаменателю (Х*(Х+20)) и избавимся от него, умножив на него все члены уравнения: 32Х + 640 + 60Х = Х² + 20Х; Х²-72Х - 640 = 0; Д=72²+4*640 = 5184+2560 = 7744; Д>0, продолжим; Х₁ = (72 + √Д)/2 = (72 + √7744)/2 = (72+88)/2 = 80 (км/час); Х₂ =72-√Д = -8 (в расчет не берем, как не имеющий смысла) Х+20 = 80+20 = 100 (км/час); ответ: скорость по шоссе 80км/час; скорость по автостраде 100 км/час; Проверка: 32/80 +60/100 = 1; 0,4+0,6=1; 1=1
Объяснение:
Данная функция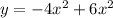
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: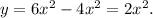
Для нахождения
единственного экстремума воспользуемся производной: 
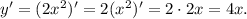
По лемме Ферма, значение производной от
экстремума нулевое. Таким образом, 
точки экстремума будет решением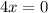 
.
Для нахождения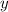
точки экстремума вычислим значение исходной функции от найденного 
:
Получается, что координаты точки экстремума это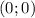
.