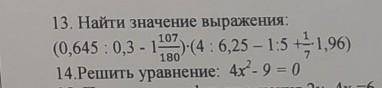
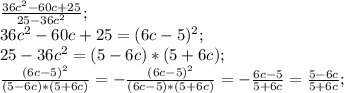
Числитель - сворачивается в квадрат разности, знаменатель - это разность квадратов.
Сворачивая по формуле квадрата разности числитель, и наоборот расписывая по разности квадратов знаменатель получаем вышесказаное выражение, далее, выносим минус за скобки, и в одной из скобок знаменателя меняем знак на противоположный, тем самым имеем право сократить с числителем. Далее, минус вносим в дробь, меняя знаки в числителе. Выходим на ответ.
Либо есть более короткий вариант решения, но тут нужна внимательность:
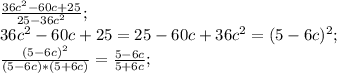
Т.к. это квадрат разности (В числителе) имеем право поменять местами 36c^2 и 25, сохраняя знаки. Свернется в тот-же самый квадрат разности, но нет заморочек с минусом.
По формуле:
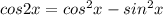
Зная это получаем:
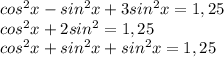
Известно что:
отсюда получаем:
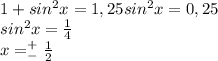
Получаем 2 уравнения:
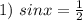это табличное значение синуса и получается 2 решения:
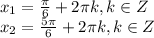
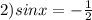аналогично получаем 2 решения:
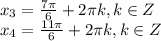
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
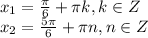
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
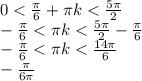
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
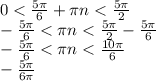
Поскольку n принадлежит целым числам, то получается что n=0,1
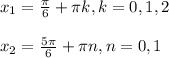
Объяснение:
14 задание