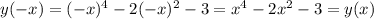
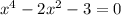
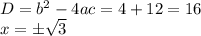
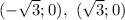точки с соью Ох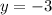
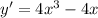
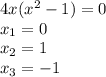
, убывает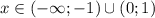 
. В точке х=-1 и х=1 функция имеет локальный минимум, а в точке х=0 - локальный максимум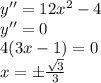
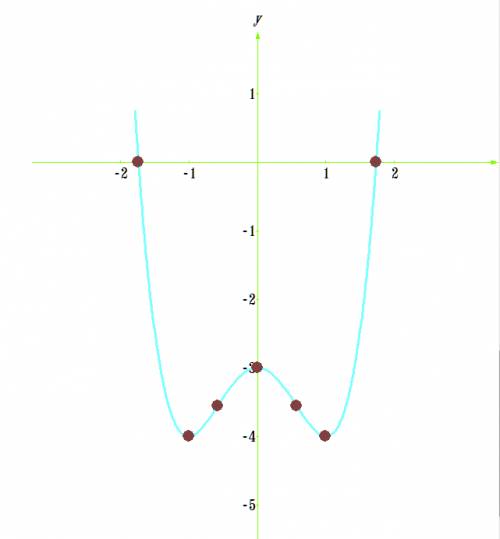
График функции х - y = 7 не проходит через точки С(5;2) и D(8;2).
Объяснение:
График функции х - y = 7 проходит через заданную точку, если при подстановке в уравнение графика функции координат х и у заданной точки получается верное равенство.
Проверяем точку С (5;2).
Её координаты: х = 5, у = 2.
х - у = 5 - 2 = 3
Так как 3 ≠ 7, то это означает, что график функции х - y = 7 не проходит через точку С(5;2).
Проверяем точку D (8;2).
Её координаты: х = 8, у = 2.
х - у = 8 - 2 = 6
6 ≠ 7 - значит, график функции х - y = 7 не проходит через точку D(8;2).
ответ: график функции х - y = 7 не проходит через точки С(5;2) и D(8;2).
Надо просто делить "столбиком" (или по другому "уголком") многочлен P(x)=x^5 +ax−7 на многочлен x+1.
Слагаемое ах переносится до конца.
В конце получаем: ax - 1 - 7 или ax - 8
ax + a ax + a
-8 - a .
Чтобы полностью разделилось, надо, чтобы остаток был равен нулю
-8 - a = 0.
Отсюда а = -8.
ответ: а = -8.